这一篇博客会比较长，目前还没写完，处于不断更新中…
这一节会用一些通俗的语言去解释一些数学上的概念，有一些解释可能并不是严谨，我们更多地是把焦点放在理解这些概念是什么，为后面的应用做铺垫。如果有一些点不能理解，也没关系，只要知道有这样一个东西就行，等真正用到的时候，有点印象，这样就会有解决问题的方向，再回来查相关的知识就可以。单纯记住一些知识是没有太多意义的，只有会应用了，才有意义。
集合 (Sets)
一堆东西，就是一个集合。例如桌子上有一堆苹果，就可以说，这是一个苹果的集合。旁边放了一堆干果，就可以说，那是一个干果的集合。这里有100个数字，都是整数，那这就是一个整数集合。
下面是一些常用的集合
ℝ实数集合 实数包含有理数 和无理数，有理数包括整数和分数，无理数就是无限不循环小数ℝ+非负实数集合 理解了实数集，这个非负实数集合就好理解了，就是把把负数去掉ℝ2有序对，像二维的坐标，就属于一个有限对，(x,y)ℝn在n维笛卡尔空间中的点ℤ整数集合S2在单位球面上的3D点
上面的这些常用的集合，大概了解一下就好了，不用详细的去探究，只要大概知道是什么，有这个名词的印象就OK，等用到的时候自然就了解了。
映射 (Mappings)
映射和编程上的函数很类似，输入参数，输出结果，或者说，给函数一个A，函数进行运算后，会返回给你一个B。而映射，类似，就是将一个东西从A变成B。
f:ℝ↦ℤ 这个东东，可以这样解释，有一个函数叫做f，这个函数呢，接收一个输入，这个输入是ℝ，也就是上面说到的实数类型的数，注意，这里是输入一个实数，而不是输入实数集合，这里的ℝ可以理解成编程函数中的数据类型。然后呢输出一个整数类型的数。基本上可以当作编程语言中的函数调用。
映射，是将一个集合中的元素，映射成另一个集合中的元素。可以说，你从A集合中找一个元素，扔进映射函数里，那么映射函数会从B集合中找一个元素，再扔给你。
逆映射 (Inverse Mappings)
通俗来讲，逆映射就是映射反过来，你从B集后找一个元素扔进映射函数，映射函数会从A集合中根据映射规则找一个元素还给你。映射中，有一个名词，叫做 双射，就是说，对于A集合中的任何一个元素，都能在B集后中找到唯一一个与它一一对应的元素，并且，对于B集后中的任何一个元素，也都在能A集合找到唯一一个与它一一对应的元素。这种情况，就叫做双射。
区间 (Intervals)
区间可以理解为一个数值范围，这个范围内的元素放在一起，也就是我们前面学到的集合。例如一周有7天，数值范围就是从星期一到星期日，某幼儿园小朋友的身高范围是80cm到140cm之间的，这些都是区间。我们从整数集合上定义一个区间，例如[1, 15]，意思就是从1到15这15个数。用中括号[] 表示的区间叫做闭区间，用小括号()表示的区间叫做开区间，还可以混合使用，例如 (] 或者 [)，这种分别叫做半开区间和半闭区间。那它们有什么区别呢？中括号，表示区间范围包含起始或结束数值，小括号表示区间范围不包含起始或结束数值。
- [1, 10] 表示区间范围是从 1到10
- (1, 10) 表示区间范围是从 2到9
- (1, 10] 表示区间范围是从 2到10
- [1, 10) 表示区间范围是从 1到9
并集: 给定两个集合A，B，把他们所有的元素合并在一起组成的集合，叫做集合A与集合B的 并集，记作A∪B，读作A并B。
交集: 给定两个集合A，B，把所有即属于A，又属于B的元素拿出来，组成一个新的集合，这个集合，就叫做A与B的 交集，记作A∩B。
区间可以做减法操作，A-B，表示的是，从区间A中，去掉属于属于区间B中的元素。
对数 (Logarithms)
我们先来看一个简单的计算 $3^{4} = 3 * 3 * 3 * 3 = 81$ 这个是不是很简单？3的4次方就是4个3连续相乘，最后结果是81。这叫做幂运算。
而对数呢，其实就是幂运算反过来，上面我们3的4次方，等于多少。而现在，我们要计算3的几次方等于81呢？用公式来表示，就是这样子的 $y = \log_381$ ，所以这里的 y 就是结果，也就是4。只要记住一句话，就很好地理解对数了，就是计算一个数的几次方等于另一个数。
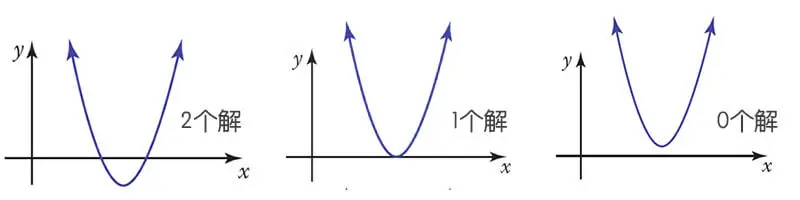
二次方程 (Quadratic Equations)
二次方程就是我们熟悉的 $ax^{2} + bx + c = 0 $ 这种类型的。我们从几何的角度来考虑这个方程，$ y = ax^{2} + bx + c $，这个方程是一个抛物线，而方程的解，就是这条抛物线与x轴的交点。有可能是0次，1次，或2次，也就是说，最终的解可能有0个，1个或两个。就像下面的图像。
角 (Angles)
一个角，是由两条射线从同一个原点，但是射向不同方向而构成的。这里，我们将角放到单位圆上来说。使用两个射线，从圆的原点出发，切割单位圆，看下面的图。
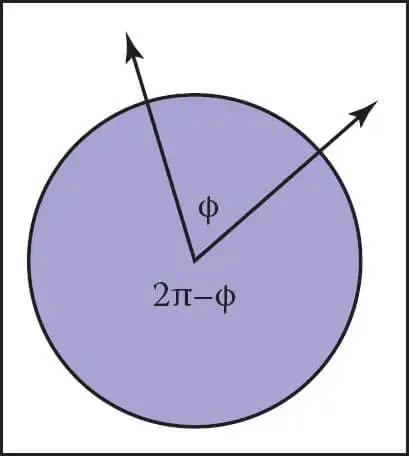
这里，我们使用的单位是弧度。弧度是基于圆的半径的纯计量单位，也就是 “半径环绕圆周” 的概念。一个整圆的弧度是 2π，也就是360度。上图中我们用两条射线去切割圆，会产生两个区域，一个大的，一个小的。通常约定是使用小的弧形，来表示角。
关于弧度和角度的换算。因为单位圆是 2π 弧度，**360 **度。所以 π 弧度就等于 180 度。所以 1弧度=180度/π
将弧度转为角度：乘以 180，除以 π
将角度转为弧度：乘以 π，除以 180
三角函数 (Trigonometric Functions)
三角函数最基本的就是我们初中学过的，正弦(sin)、余弦(cos)、正切(tan)，而这些三角函数，都是基于 直角三角形 而建立的。
看下面一个直角三角形的图，我们先把三条边的的名字标注上
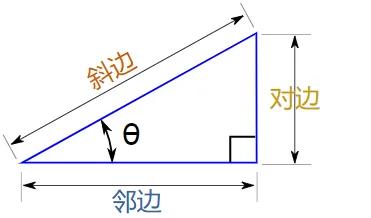
对于直角三角形中某一个角θ来说，
- 对边，就是对面的边，
- 邻边，就是旁边的边，
- 斜边，就是整个三角形最长的边。
而上面提到的三个基本的三角函数，就和这三条边有关。
正弦 $sin(θ) = \frac{对边}{斜边}$
余弦 $cos(θ) = \frac{邻边}{斜边}$
正切 $tan(θ) = \frac{对边}{邻边}$
其实就是用一条边的长度除以另一边的长度。 关于三角函数就暂时介绍这么多，其实里面还有很多内容，这个我想等在图形学中用到时，再详聊这方面的内容。
向量 (Vector)
向量在图形学和游戏开发中有大量的应用 ，那么什么是向量呢？其实就是一个方向，或者说一个偏移！例如，用手指指向天空中某颗流星，这就是一个方向。有一个人问你，超市在什么地方，你说，从这里出发，向左走50米，然后向前走30米，这里就有了两个向量，一个指向左边，一个指向前面。
向量是有大小的，上面说的向左走50米，这里的50就是可以理解为大小。
两个向量，只要方向相同，大小相同，那就是一样的，和向量的起点无关。
向量，与坐标系是息息相关的。现要只要记住，向量是偏移，是方向，就可以，不管怎样的数据结构去标识，不要把值理解成一个点就可以。
向量的操作 (Vector Operation)
向量可以相加，相减，相乘。这里我们暂时只讨论加和减。
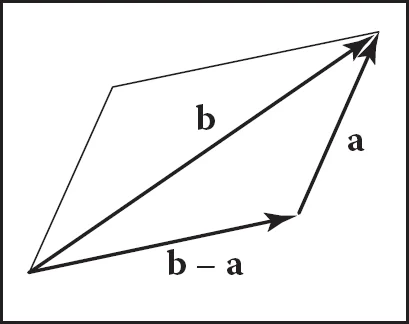
两个方向相加，会得到什么呢？假设你站在A点，然后向左走了50米，到达B点，然后从B点又向前走了30米，到达C点。这里有两个向量一个是从A点到B点的向量，我们表示成，$\vec {AB}$。第二个向量是从B点到C点，我们表示成 $\vec {BC}$。那两个向量相加的结果呢，就是一个从A点指向C点的向量，我们表示成 $\vec {AC}$。
向量相加，不管中间加了多少向量，最后的结果，都是从最初的起点指向最后的终点的一个向量。看下面的图
两个向量相减，会得到一个从被减向量的头，指向减向量的头。例如有两个点，A和B，A-B，就会得到一个从B点指向A点的向量。这个是很有用的，例如在游戏中你要计算炮弹射向敌人的方向，只需要用敌人的位置，减去炮口的位置，然后将结构标准化，就会得到炮弹的发射方向。
负向量就是一个向量大小相同，方向相反的一个向量，例如你现在朝东，那负向量就是朝西。
向量可以表示成行向量，或者列向量。
这是一个列向量 $a = \begin{bmatrix} x_{a} \\ y_{a} \end{bmatrix}$
这是一个行向量 $a = \begin{bmatrix} x_{a} & y_{a} \end{bmatrix}$
向量的大小(模)
向量的大小，也叫做向量的模，怎么计算呢？例如一个向量是这样的 $a = \begin{bmatrix} x_{a} & y_{a} \end{bmatrix}$，向量的模，是一个标量，通俗点来讲就是一个数。向量的模用双竖线表示，直接看下面的计算公式
$\lVert x \rVert = \sqrt{x_{a}^2 + y_{a}^2} $
就是向量中的每一个元素平方和，然后开平方
向量的点积
向量的点积，是两个向量之间的关系，与两个向量的大小，以及它们之间的夹角有关。看下面有两 a, b 两个向量的一个图
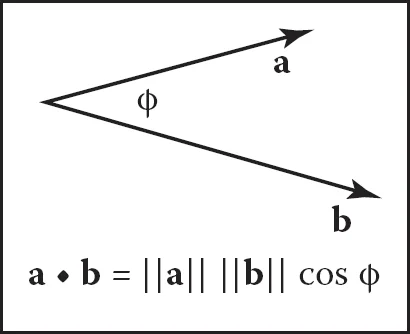
向量的点积公式就是图中的，点积的是由两个向量的模以及两个向量之间夹角的 cos 值相乘得到的。
如果两个向量都是单位向量，那它们模就是1，最后会得到向量的点积，就是夹角的cos值。
上面是向量点积的几何定义，还有一个代数定义的公式，用来计算点积的值。
$a \cdot b = \sum_{i=1}^{n}a_{i}b_{i}$
就是两个向量对应元素乘积的累加和。这个公式算出来的结构，和上面那个几何公式的结果是一样的。
现在基本上游戏引擎中都有直接计算点积的API，或者数学库，不用自己手写公式。
点积有什么用呢？主要有两方面的应用，一是可以大概判断两个向量的方向，是相同，垂直，还是相反。二是可以用来计算一个向量在另一个向量上的投影。这里只要大概有个印象就行，后面等用到了再细说。
向量的叉积
这里引用维基百科上对于向量叉积的解释，我觉得这个解释很清晰，很易懂。
叉积（英语：Cross product）又称向量积（英语：Vector product），是对三维空间中的两个向量的二元运算，使用符号$\times$。与点积不同，它的运算结果是向量。
就是说向量的叉积是由两个向量进行叉乘运算得到的，结果也是一个向量，而这个向量呢，是垂直于那两个向量的。有一条很重要的规则是，如果两个向量方向相同或相反，亦或任意一个的长度为零，那么它们的叉积为零。看下面的图
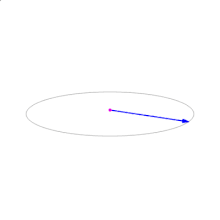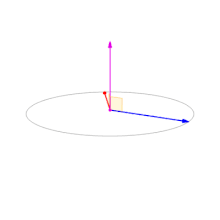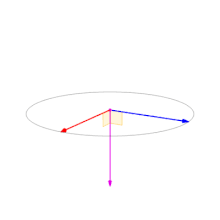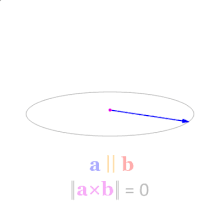上图中叉积a × b（垂直方向、紫色）随着向量 a（蓝色）和 b（红色）的夹角变化。 叉积垂直于两个向量，模长在两者平行时为零、在两者垂直时达到最大值‖a‖‖b‖。
如果两个向量a，b分别是指向x轴和z轴方向，则叉积向量会有两个方向，要么指向上方，要么指向下方，那这个是由什么决定的呢？
将右手食指指向 a 的方向、中指指向 b 的方向，则此时拇指的方向是向上的。将右手食指指向 b 、中指指向 a ，那么拇指就必定指向相反方向，即翻转了叉积的符号。
叉积可以用于计算法向量。
计算公式: $(x_1, y_1, z_1) \times (x_2, y_2, z_2) = (y_{1}z_{2} - z_{1}y_{2},z_{1}x_{2} - x_{1}z_{2},x_{1}y_{2} - y_{1}x_{2})$