经常有小伙伴想系统地学习一下数据结构,但很难找到适合自己的教程。好吧,其实说的是我自己。那今天就来聊一聊这个问题。
我们先把一些常用的数据结构列表出,大概讲一下他们的结构及应用,后面分篇细细讲解。在分篇讲解时,我们的关注点是某个数据结构是什么,怎样用代码描述出来。而更多涉及到这个数据结构的一些算法,将在后面的算法系列中详细讲解。
这个系列的博客,是面向那些和我差不多,大概了解数一些数据结构(知道一些名字,不太了解内部详细实现),又想系统地巩固一下,深入一下的小朋友们~
快来一起学习吧 ^_^
数组 [Array]
数组用于存储同种类型的数据,数据与数据之间在内存中是连续的(相邻的),在使用数组前,要预先分配好指定的内存大小。
应用: 例如我们想存储幼儿员小班所有小朋友有的名字,就可以用数组。 [第一个小朋友名字, 第二个小朋友名字, 第三个小朋友名字, …]
链表 [Linked List]
链表,是由一个个节点,相连而成。每一个节点,都是独立的元素,它们在内存中的位置也不一定是连续的。每一个节点,都拥有两个部分,数据部分,和一个指向下一个节点的引用。刚刚说的是单向链表。
还有一种叫做双向链表,区别就是一个节点有三个部分,数据部分,一个指向下一个节点的引用,一个指向上一个节点的引用。
还有一种叫做循环链表,区别就是尾部和头部会连起来。
应用: 链表常应用于存储不能事先确认数据个数的情况,对于这种情况,使用链表不需像数组一样预先分配内存,当有新的数据要存储时,只需要新申请一个节点的内存空间,然后将这个节点添加到链表即可。
堆栈 [Stack]
想象这样一个场景,往一个箱子里放书,先放进一本漫画书,再放进一本故事书,再放进一本数学书。现在最上面的是数学书,如果要把里面的书一本一本都拿出来,就要先拿出数学书,再拿出故事书,再拿出漫画书,正好与放下的顺序相反。这就叫先进后出,FILO (First in last out)。
而堆栈就是这一种结构,堆栈通常拥有两个方法,Push 和 Pop,分别就是放入数据,和拿出数据。后放入的数据,总是在最上面,往外拿数据时,也像从箱子里拿书一样,要从最上面开始拿。是不是很形象~
应用: 堆栈是一个很有用的东西,我们平常用的很多软件中,都能找到它的应用,例如文本编辑器的撤销功能,其实就是在特定时间将用户的操作Push入栈,然后撤销时,从栈中Pop出最近的一个操作。再例如浏览器的后退功能,也是依次将用户浏览的网址Push入栈,然后后退时,依次Pop出最近的浏览网址。
队列 [Queue]
大家排队买冰激凌,就是一种队列结构,这个人买完冰激凌,然后下一个。在这个过程中,后面不断的有人在排队,队伍越来越长,服务员从前面一个一个处理顾客的需求。
队列也是这样,先入列的,也会先出列,就像排队。先排队的,先拿到冰激凌,然后走人。所以队列通常有两个操作,入列(Enqueue) 和 出列 (Dequeue)。队列是先进先出,FIFO (First in first out)。
还有一种队列叫做环形队列,会循环利用已经分配好的内存空间,而不是入列和出列时执行分配和销毁内存操作。
应用: 需要依次处理的事情,都可以使用队列,例如网络通信数据包,当客户端收到消息时,就可以放入队列,而消息处理器,不断地尝试从队列中取消息,如果有,则处理。
咦?刚才好像说到冰激凌了~
二叉树 [Binary Tree]
树,就像我们平时在公园里看到的那种树的结构,分叉。而二叉树呢,就是只能分两叉,一分为二,每一个分叉,又可以最多一分为二。就像下面的这种形状。
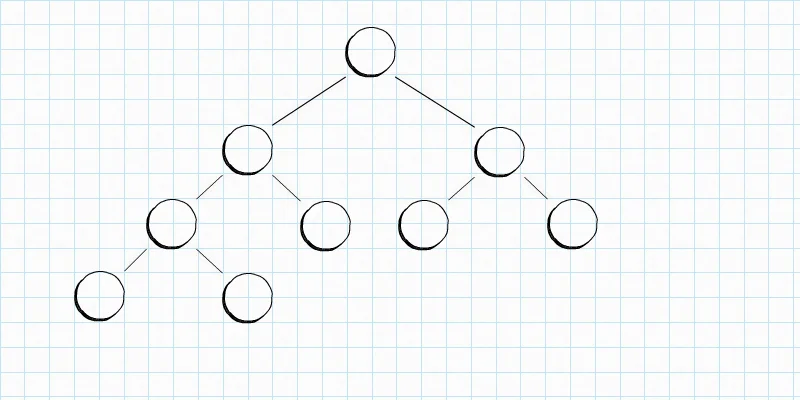
二叉树的结构,也可以理解为由 “节点” 组成,就像链表那样的节点。对于二叉树来说,每一个节点有三个部分,数据部分,指向左边分叉节点的引用,指向右边分叉节点的引用。
二叉树,每一个节点,最多能分两叉,也就是,每一个节点,最多拥有两个直接子节点,也可能有一个,也可能没有。其实,二叉树的实现,很多也是用链表来做的。这个后面的博客再详细介绍,嘿嘿~
应用: 树型结构在计算机中也有很多应用,例如我们很熟悉的文件浏览器。一个目录下,可以有多个目录,子目录下,又可以有多个文件,然后还可以再分叉继续往下深入。不过,真正的文件系统并不一定用的是二叉树,也可能是n叉树,具体的我还不是很清楚,尴尬ing…
二叉查找树 [Binary Search Tree]
二叉查找树,简称 BST,是在二叉树的基础上,增加了额外的规则。首先,我们给每一个节点赋予一个权重,这个权重,可以用任何东西代替,例如小朋友的分数,例如冰激凌的价格等等。然后,每一个节点,满足下面的规则
- 如果一个节点左子树不为空,则整个左子树上的所有节点,权重都要小于当前节点
- 如果一个节点右子树不为空,则整个右子树上的所有节点,权重都要大于当前节点
- 左右子树,也都是二叉查找树,也就是说,子树,也要满足上面也条规则
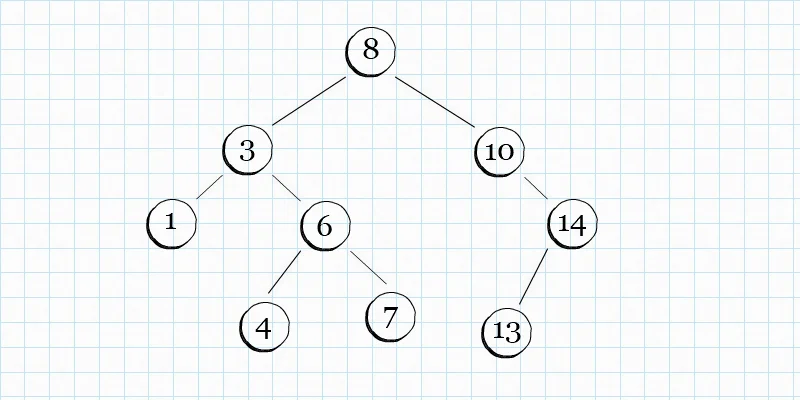
应用: 二叉查找树常常应用一些需要数据保持有序状态,但是又经常需要插入和删除某些数据的场景。例如电商平台中的商品数据组织,可能就经常用到二叉查找树。
二叉堆 [Binary Heap]
是不是已经有点混乱了?没关系,只要大概了解有这样一个东西就行,不用完全理解是什么,怎么用。哈~,现在来说继续说一下二叉堆。二叉堆也是树…
要说二叉堆,就不得不说一下完全二叉树。因为二叉堆,首先得是一颗完全二叉树,什么是完全二叉树呢?就是一颗树除了最后一层节点外,其他层,必须拥有左右两个节点,不能左节点为空,或右节点为空。而对于最后一层的节点,也就是上面说的叶子节点,都要尽可能地靠左。这个尽可能地靠左有点抽象,我们看下图就会明白。
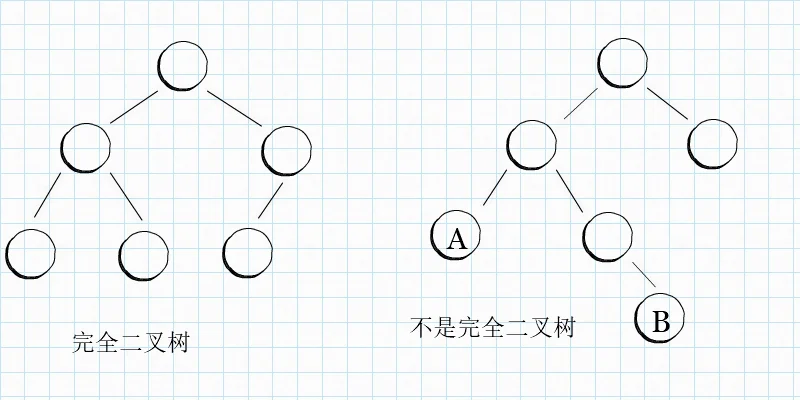
然后二叉堆,分为最大堆和最小堆。对于最大堆来说,任何一个节点的值,都要大于等于左右两个子节点。而最小堆,任何一个节点的值,都要小于等于左右两个子节点。下面上图,嘻嘻~
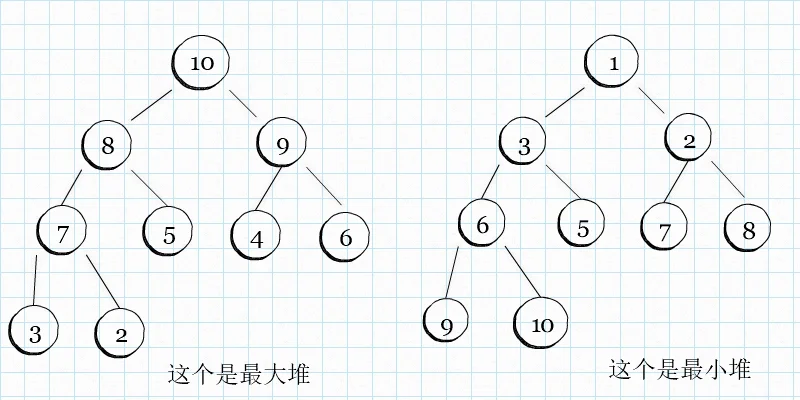
应用: 二叉堆可以用于实现优先队列,而优先队列在操作系统中,可以用于处理任务的调度工作。
终于说完树了,感觉自己已经丢失了萌,只剩下呆了,要不吃包薯片吧。我不胖!~
散列/哈希 [Hashing]
什么Hash呢?Hash可以理解为一个唯一标识,这个标识可以是一个字符串,或者一个数字,只要唯一,都可以。那什么是Hash函数呢?Hash函数就是用于产生Hash值的东西,你向这个函数输入一些数据,这个函数就会返回给你一个Hash值。就像榨汁机,丢进橙子去,出来的一定是橙汁,丢进桃子去,出来的一定是桃汁。这是一一对应的关系,这个函数,不管执行多少次,只要输入的数据相同,输出的Hash值一定相同。
一些编程语言中,拥有字典的结构,就是一个Key,对应一个Value,其实就可以理解为是Hash表。那Hash表有什么用呢?可以通过Key快速地访问对应的数据,而不用像数组那样,需要去遍历。例如幼儿圆小朋友的身高,就可以以名字作为Key,以身高作为Value,存储在一个Hash表中,这样可以快速地查询某一个小朋友的身高数据。
这里就有一个问题,万一小朋友有重名的怎么办?Hash函数也是存在这个问题的,就是输入两个不同的数据,但是产生的Hash值是一样的,这叫做碰撞。这个问题,有很多种解决方案,我知道的一个是,将所有碰撞的Value,以一个链表的形式存储起来。
这个东东就先说到这里,有一些东西我也不太懂,等后面我学会了,就写篇专门讲解Hash的文章,嘻嘻~
图 [Graph]
现在来说一下图,这里的图,可不是我们平时理解的图片,而且是一种由点,和连接点的边而构成的一种数据结构。看下面的图
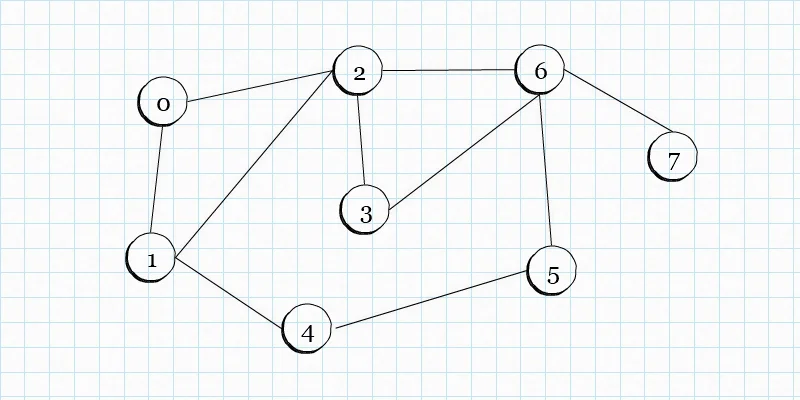
上面的图片,就是一种图的结构。图中的圆圈,就是图结构的节点,我们称为 node,而连接节点的线,就是边,我们称为 edge。有没有感觉,图结构,很像地图上的城市和道路?对的,其实图结构,在我们平常用的地图应用中,就用到了,可以用来计算两个点之间的最短距离。
上面的图中,0这个点,连接着1和2,意思就是可以从0,到达1和2。而5这个点,和6,4相连,就是说可以从5这个点,到达6和4点。点与点之间的边,我们可以赋予权重,来表示一些信息。例如3与2这个点的边,我可以赋予一个表示距离的权重,假设是10,而3和6这两个点之间也赋予一个表示距离的权重,例如16,这样,就可以计算一些东西。
那么,图在计算机中应该怎样去表示呢?有两种常用的结构,一种是矩阵,一种是邻接表。这个我们后面专门的文章再详细讲解。
前缀树/字典树 [Trie]
这个东东,和树和相似。维基百科中的解释是,一个节点的所有子孙都有相同的前缀,也就是这个节点对应的字符串,而根节点对应空字符串。我们看一个图,就会大概明白一些。
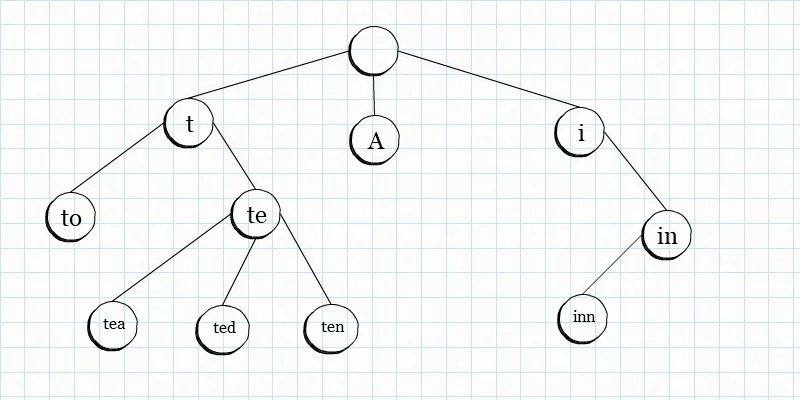
Trie是一种很有效率的数据结构,用于在字典中查找指定的词,它的效率,比BST(二叉查找树)还快。Hash表结构也提供了相同速度的查找效率,但是Trie没有Hash碰撞的问题。用Trie还有一个好处是,我们可以以很快的速度找出所有以指定前缀开头的词,这个,Hash可是做不到。但是Trie也有缺点,就是需要很多额外的内存空间,相当于用空间换取了效率,不过,对于这个问题,也有很多优化方案,后面等我学会了再详细讲解。
应用: 有一个我们很熟悉的应用,我们在浏览器中输入网址时,不用完全输完,就是弹出一些类似的历史网址,这个就可以用Trie实现。还有搜索框中搜索东西,我们输入一个字的时候,就会弹出好多以第一个字开头的东西,随着后面再输入内容,匹配的内容也会变化。
线段树 [Segment Tree]
你知道二分法吗?就是把一堆糖果,先分为两份,然后将这两份,每一份再分为两份,然后再分为两份,然后… 就可以吃掉它了,嘿嘿~
认真起来,将 0~10 这11个数,先分为两份(就是用数的个数除2,如果除不尽,就向下取整呗),第0个到第五个为一份,第6个到第10个数为一份。然后再分,看下面的图。

请注意: 上面说的 第几个第几个,是指所引,这里我们为了方便计算,才使用了0~10这个数,每一个数正好与索引相同。我们关注的是 索引 第0个数具体是什么,不重要,可以是 100 也可以是10000
上图中的每一组数,可是不是感觉可以看成一个节点?然后连起来,就成了我们之前学过的树的结构了,对不对,没有记起来的话就看一下之前的内容,复习一下噢~
下面开始说线段树了,将上面的每一组数作为一个节点,然后将每一个节点中的数加起来,作为节点的值,就像下面的图这样。这就是线段树。线段树,是一种特殊的二叉树,每一个节点不只代表一个数,而是代表一段区间。
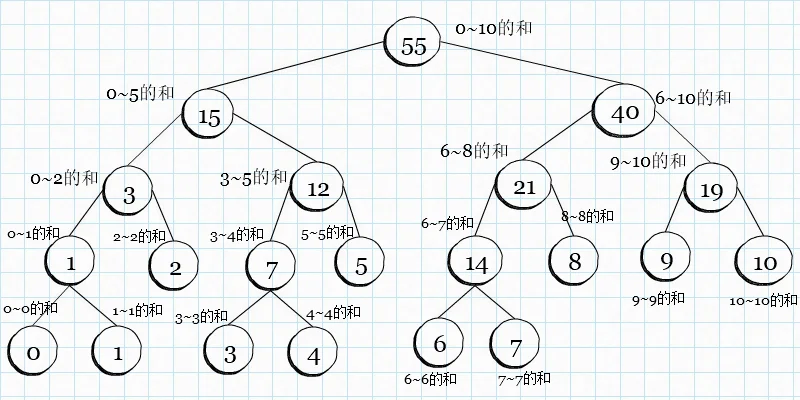
对于线段数的解释,就到这里,只要知道线段树中的节点,表示的是一个区间就可以了,更详细和具体的内容,我们后面再详细学习。如果看不懂上面的概念解释,推荐另一个小朋友写的一篇不错的博客,解释的很清楚 > 点这里查看 :)
后缀树 [Suffix Tree]
后缀树可以解决很多关于字符串的问题例如匹配和查询相关的问题,但是描述起来相对来说比较复杂,这里就不解释了,有文章总结的一句话是 一个给定的文本text的后缀树就是一个压缩的后缀字典树
后面我们使用专门的一篇文章去解释关于后缀树的内容。
到这里基本的数据结构概述就算结束了,当然,这里提到的结构并不能覆盖所有的数据结构,每一种数据结构,可能还可以分出很多变化模式来,例如字典树,在此基础上还有压缩字典树等等。
学习不是一蹴而就的,要一步一步来,所以,我们接下来就一步一步来学习数据结构相关的东西 ^_^。