这篇博客来聊一下二叉树。呆萌数据结构系列,终于开始了树型结构的部分。这篇文章你能够学到的内容有 树,有哪些应用,二叉树的结构,什么是满二叉树,什么是完全二叉树,二叉树的遍历方式,二叉树的构建。二叉树是很基本的结构,在此基本上,会有很多很多变种,变成各种各样的树,理解了二叉树,对于后面学习其他更复杂的树型结构,会有很大的帮助。
这篇文章首先理解文字上的内容,不要管代码,对二叉树的结构,操作,理解原理,最后再看代码。
好了,下面开始吧。
树,有哪些应用
现在学习的目的,已经不是为了考试,而是为了能够用来做一些事情。对于我们来说,知识只有用起来,才是有意义的,所以,我们先说一下树型结构的一些应用。咦?为什么不是二叉树的应用呢,因为很多应用,都不是单纯地使用二叉树来实现的,而是在此基础上,使用了它的变种,所以我们这里直接说一下树型结构的一些应用。
我们使用各种各样的数据结构,本质上似乎就是为了更方便或更高效地去组织数据,操作数据。我们平时用的搜索引擎,当你输入要搜索的内容时,可能在输入了前几个字,下面就已经出现了我们想要的结果,其实背后,就是用了树型结构,才能在这样庞大的数据中,找到与我们输入内容匹配的结构。
我们手机中常用的电话薄,也是这个原理。当你找一个联系人时,输入第一个字,例如李,可能下面的结构是李四,李五,李六,但是输入第二个字时,结果就会更精确。
我们平时用的压缩软件,其数据压缩算法,也离不开树型结构。
操作系统中的文件系统,以及我们使用的数据库软件,也是树型结构的应用。
二叉树的结构
二叉树是由一个一个节点组成,每个节点,有数据部分,以及两个节点指针,一个指向左子树,一个指向右子树。二叉树每一个节点,最多拥有两个子树。就像下面中的图(图中的数字可以理解为要存储的数据)。另外,二叉树的分支,也就是左右子树,是具有左右次序的,不能随意颠倒。
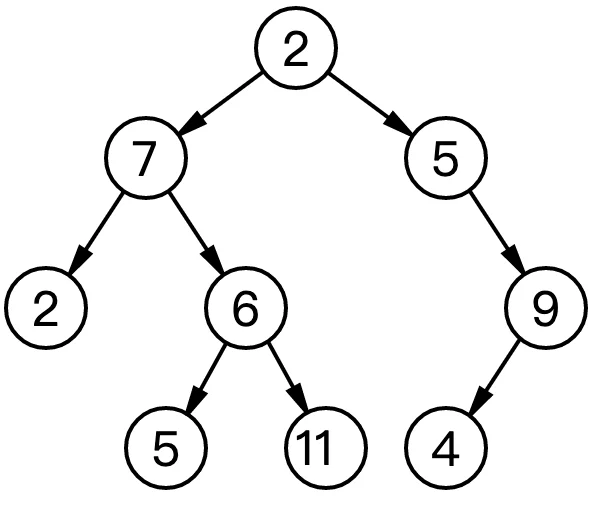
什么是满二叉树
满二叉树就除了最后一层,每一个节点,都拥有左右两个子树,没有空缺。
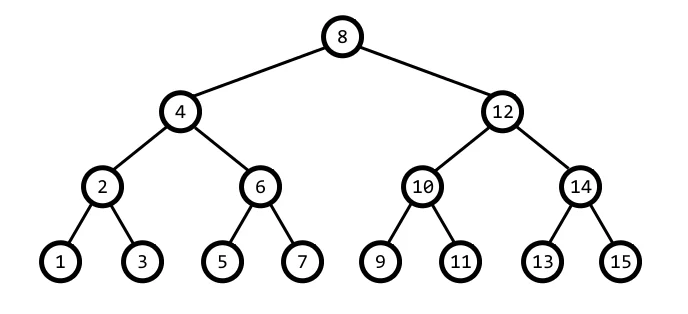
什么是完全二叉树
在理解了满二叉树的基础上,才能理解完全二叉树。完全二叉树要满足两个条件。首先,如果不看最后一层,那这棵树是满二叉树。其次,最后一层,要尽可能的往左靠,中间不能有空缺。什么意思呢?我们看一张图。
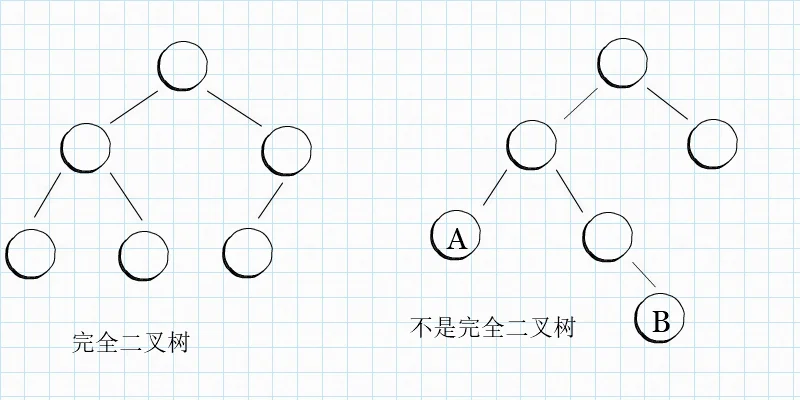
上图中,左边的图是一个完全二叉树。如果去掉最后一层,那这棵树是满二叉树,满足。最后一层,即使缺少了一个节点,但是所有的节点都是尽可能地往左靠了,所以,也满足第二个条件。
而第二个图,不是完全二叉树。首先第一个条件就不满足。其实,最后一层的节点也不是尽可能地往左靠。什么叫尽可能得往左靠呢,如果 B 节点作为 A 节点的左子树,那就叫做尽可能地往左靠了。
二叉树的遍历方式
树的遍历(不限于二叉树),有广度优先遍历,和深度优先遍历。而深度优先遍历,分为前序遍历,中序遍历,后序遍历。
我们以下面这张图为例子,分别说一下这几种遍历方式。
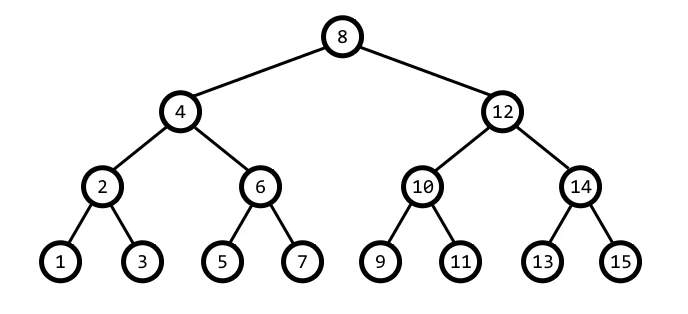
广度优先遍历:
广度优先遍历,其实就是一层一层地遍历,所以又可以称为层次遍历,会先访问离根节点最近的节点。按照广度优先遍历,上面的树中节点访问顺序是这样的。
8,4,12,2,6,10,14,1,3,5,7,9,11,13,15
深度优先索索 深度优先搜索,通常采用递归的形式来进行。这里我们用简单的代码去描述,会比文字描述更直观。
前序遍历 前序遍历的顺序是先访问根节点,然后再访问子树。
void pre_order_traversal(Node root) { // TODO:操作当前节点 // 如果左子树不为空,则递归处理左子树 if(root.left != null){ pre_order_traversal(root.left); } // 如果右子树不为空,则递归处理右子树 if(root.right != null){ pre_order_traversal(root.right); } }中序遍历 中序遍历的顺序是先访问左(右)子树,然后访问根,然后访问右(左)子树。
void in_order_traversal(Node root) { // 如果左子树不为空,则递归处理左子树 if(root.left != null){ in_order_traversal(root.left); } // TODO: 处理当前节点 // 如果右子树不为空,则递归处理右子树 if(root.right != null){ in_order_traversal(root.right); } }后序遍历 后序遍历的顺序是先访问子树,然后再访问根。
void post_order_traversal(Node root){ // 如果左子树不为空,则递归处理左子树 if(root.left != null){ post_order_traversal(root.left); } // 如果右子树不为空,则递归处理右子树 if(root.right != null){ post_order_traversal(root.right); } // TODO: 处理当前节点 }
仔细看上面的代码已经注释,可以发现三种遍历方式都是递归的方式,基本类似,主要区别,是
什么时候处理当前节点。
按层次顺序构建上图中的二叉树
import queue
class Node:
def __init__(self, data):
self.data = data
self.left = self.right = None
# 二叉树构建函数(按层次构建)
def construct_in_level_order(data_queue):
if data_queue is None or data_queue.empty():
return None
# 创建 Root 节点
root = Node(data_queue.get())
# 创建一个队列,用于按层来构建二叉树
node_queue = queue.Queue()
# 将 Root 节点先放入节点队列中
node_queue.put(root)
while not node_queue.empty():
# 从队列中拿出一个节点作为当前节点
node = node_queue.get()
# 创建当前节点的左子树节点
left_node = None
if not data_queue.empty():
left_node = Node(data_queue.get())
node.left = left_node
# 创建当前节点的右子树节点
right_node = None
if not data_queue.empty():
right_node = Node(data_queue.get())
node.right = right_node
if left_node is not None:
node_queue.put(left_node)
if right_node is not None:
node_queue.put(right_node)
return root
# 二叉树层次遍历函数
def level_order_traversal(root):
q = queue.Queue()
if root is not None:
q.put(root)
while not q.empty():
node = q.get()
if node.left is not None:
q.put(node.left)
if node.right is not None:
q.put(node.right)
print(node.data)
if __name__ == '__main__':
data_queue = queue.Queue()
arr = [8, 4, 12, 2, 6, 10, 14, 1, 3, 5, 7, 9, 11, 13, 15]
for item in arr:
data_queue.put(item)
root = construct_in_level_order(data_queue)
level_order_traversal(root)
如何删除一个节点
删除一个节点,就是将某一个节点从整个树中踢除掉,重要的是,踢除某个节点后,需要调整整棵树的结构,这个要根据不同的规则去做。最简单的方法就是,删除某一个节点后,让左子树或右子树,上升成为替换删除掉的节点,改变对应的指针。具体的代码实现,我们将在后面其他树型结构的文章中介绍。
更多内容
二叉树的结构我们先介绍到这里,后面还会有更多更复杂的关于树的结构,我们慢慢来,循序渐进。
还有一些关于二叉树很不错的文章,推荐给大家