今天我们来说一下二叉堆(BinaryHeap)。堆是很有用的数据结构,例如后面会学到的优先队列,堆排序等,都和堆有关。操作系统中很多调度,也和堆有关。
还记得我们之前学过的完全二叉树吗?如果不记得了,就需要先回去复习一下,因为二叉堆,首先是一棵完全二叉树,或者近似完全二叉树。
再来说一下二叉堆的特性。二叉堆分为最小堆和最大堆。如果是最小堆,那么父节点的值,总是小于或等于任何一个子节点的值,通俗点就是把一棵树从上往下看,值在变大,下面的大于等于上面的。如果是最大堆,则是反过来,父节点的值,总是大于或等于任何一个子节点的值。
如果要简单点记忆,那就是这棵树上的值按层来看,如果是从小到大,那就是最小堆,如果是从大到小,那就是最大堆。
接下来我们就开始说二叉堆的细节,插入节点,删除节点。
插入节点
插入节点,其实也就是构建二叉堆的过程,语言描述流程如下。
- 找到要插入的位置,这个位置就是当前这棵完全二叉树,最后一个位置 (不太好理解)。如果用代码流程来描述的话,就是按层遍历当前的树,如果遇到一个节点,左子树为空,或者又子树为空,或者左右子树都为空,那么,这个点就是要插入节点的父节点,而要插入的节点,将作为这个节点的左子树或右子树。看下面的图
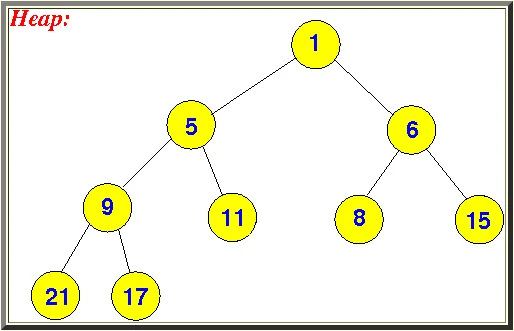
假设我们要在上面的堆中插入一个节点,按照上面代码流程中描述的,可以找到要插入节点的父节点,是11。
- 找到了要插入节点的父节点,还要判断这个父节点是左子树为空,还是右子树为空,还是都为空,如果左子树为空,则新点作为左子树,如果左子树不为空,则新点作为右子树。插入后的图如下(假设要插入的数值为3)
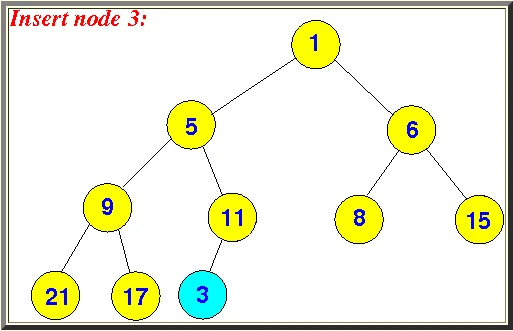
- 节点插入后,当前的树并不满足二叉堆的规则,所以还需要将新插入的点向上浮动。如果当前节点值小于父节点的值,则交换当前节点和父节点的值。然后再次判断,直到当前值不再小于父节点值,或者父节点值为空了,则位置调整完毕,整个插入流程也就结束了。看下面的流程图

上图中,首先用 3 和 11 比较,因为 3 小于 11,所以交换两个节点的值

上图中,再次用 3 和父节点 5 比较,因为 3 小于 5,所以再次交换两个节点的值

上图中,再次用 3 和父节点 1 比较,咦,3 不小于 1,所以不交换,节点调整结束。此时的树满足二叉堆的规则。
以上就是整个插入节点的流程,下面我们用代码去实现一下。代码中的 TreeAlgo 类是我们为了方便写的一个帮助类,实现了层序打印和查找的一些方法。
// 定义节点的结构
public class Node {
public int data;
public Node parent = null;
public Node left = null;
public Node right = null;
public Node(int data){
this.data = data;
}
}
// 定义二叉堆操作类
using System;
public class BinaryHeap {
public Node root;
public void Insert(int data){
Node lastParentNode = TreeAlgo.FindParentOfFartestLeftLocation(root);
if(lastParentNode == null){
Console.WriteLine("Insert Root Node " + data);
root = new Node(data);
}else{
Node newNode = new Node(data);
if(lastParentNode.left == null){ // 如果左子树为空,则插入到左子树
lastParentNode.left = newNode;
} else if(lastParentNode.right == null){ // 如果右子树为空,则插入到右子树
lastParentNode.right = newNode;
}else{
Console.WriteLine("父节点错误,父节点左右子树都不为空,无法插入!");
return;
}
newNode.parent = lastParentNode;
Node opt = newNode;
// 以最小堆的方式插入节点,即父节点小于等于子节点
// 如果是以最大堆的方式插入,则父节点要大于等于子节点 只要将 <= 改为 >= 即可
while(opt != null && opt.parent != null && opt.data <= opt.parent.data){
int tmp = opt.data;
opt.data = opt.parent.data;
opt.parent.data = tmp;
opt = opt.parent;
}
}
}
}
// 运行刚才写的代码
using System;
using System.Collections.Generic;
class Program
{
static void Main(string[] args)
{
BinaryHeap bh = new BinaryHeap();
bh.Insert(1);
bh.Insert(9);
bh.Insert(22);
bh.Insert(17);
bh.Insert(11);
bh.Insert(33);
bh.Insert(27);
bh.Insert(21);
bh.Insert(19);
TreeAlgo.LevelOrderTraversal(bh.root);
}
}
// TreeAlgo 帮助类代码
using System;
using System.Collections.Generic;
public static class TreeAlgo {
// 层序遍历树,打印出的内容,括号里面是父节点的值
public static void LevelOrderTraversal(Node root){
if(root == null){
return;
}
Queue<Node> q = new Queue<Node>();
q.Enqueue(root);
while(q.Count > 0){
Node currNode = q.Dequeue();
string msg =string.Format("{0}({1}) ", currNode.data, currNode.parent != null?currNode.parent.data.ToString():"null");
Console.WriteLine(msg);
if(currNode.left != null){
q.Enqueue(currNode.left);
}
if(currNode.right != null){
q.Enqueue(currNode.right);
}
}
}
// 按层遍历,获取第 index 个节点
public static Node GetIndexOfNodeWithLevelOrder(Node root, int index){
if(root == null){
return null;
}
Queue<Node> q = new Queue<Node>();
q.Enqueue(root);
int iIndex = 0;
Node targetNode = null;
while(q.Count > 0){
Node currNode = q.Dequeue();
if(iIndex == index){
targetNode = currNode;
break;
}
if(currNode.left != null){
q.Enqueue(currNode.left);
}
if(currNode.right != null){
q.Enqueue(currNode.right);
}
iIndex += 1;
}
return targetNode;
}
// 获取按层遍历时,最后一层的最后一个节点
public static Node GetLastNodeOfLevelOrder(Node root){
if(root == null){
return null;
}
Queue<Node> q = new Queue<Node>();
q.Enqueue(root);
Node lastNode = null;
while(q.Count > 0){
lastNode = q.Dequeue();
if(lastNode.left != null){
q.Enqueue(lastNode.left);
}
if(lastNode.right != null){
q.Enqueue(lastNode.right);
}
}
return lastNode;
}
// 按层序遍历,只要任何一个节点左子对为空,或右子树为空,则为要找的点(前提是这棵树必须为完全二叉树)
public static Node FindParentOfFartestLeftLocation(Node root){
if(root == null){
return null;
}
Queue<Node> q = new Queue<Node>();
q.Enqueue(root);
Node targetNode = null;
while(q.Count > 0){
targetNode = q.Dequeue();
if(targetNode.left == null || targetNode.right == null){
break;
}
q.Enqueue(targetNode.left);
q.Enqueue(targetNode.right);
}
return targetNode;
}
}
上面的代码可以自己使用C#运行一下看结果。下面我们继续说删除节点的操作。
删除节点
删除节点,稍微复杂一点点,但也不是特别复杂,按下面的流程来操作即可
- 找到按层序遍历的最后一个节点,然后用最后一个节点的值,替换要删除节点的值。然后将最后一个节点值删除掉。看下面的图
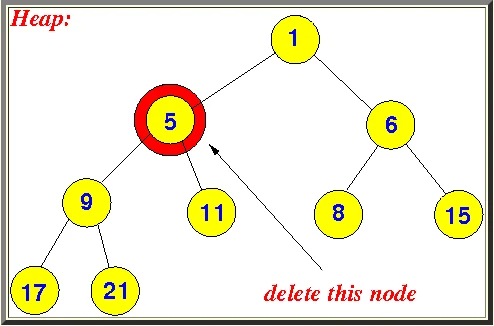
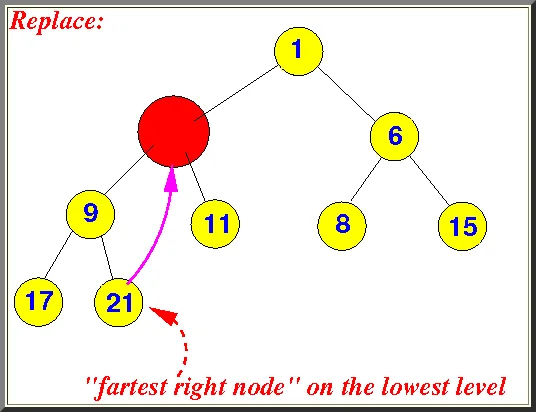
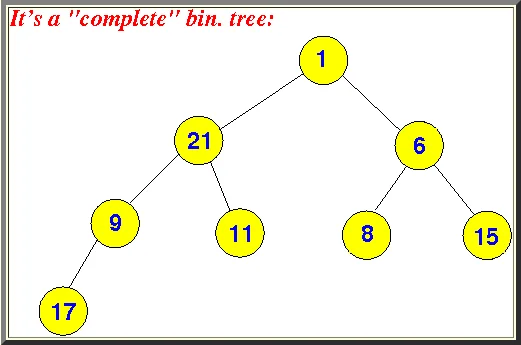
上面的过程,我们已经将最后一个节点 21 替换到了要删除的节点 5 的位置,并且将原来 21 的节点从树中删除掉。但是现在的树不符合二叉堆的规则,所以我们需要浮动现在的 21 节点。
- 浮动节点,将树调整为正确的二叉堆。删除节点时,节点的浮动有可能需要往下浮动,也有可能需要往上浮动。我们当前所讲的,都是按最小堆来操作的。如果 21 节点比父节点小,则要往上浮动。如果 21 节点比父节点大,则要往下浮动。
往上浮动,只要循环判断是否比父节点小即可,就像插入节点那样。而往下浮动,可能面对着两个又节点,所以要选择和两个子节点中值小的那个节点进行数据交换。显然,现在的 21 节点需要往下浮动,浮动到没有子节点,或者没有比当前节点小的节点位置。

上图中,21 的子节点 9 和 11,需要和值更小的 9 进行交换

上图中,21 换到了原来 9 的位置,发现还有子节点,所以继续判断。因为 17 比 21 小,所以需要继续交换。
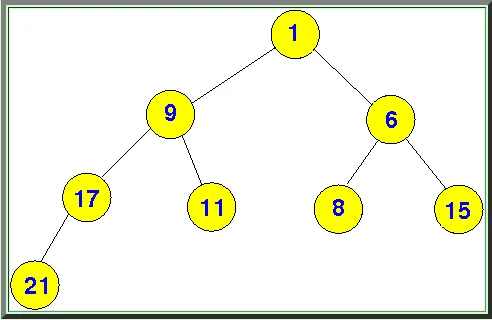
到此,发现没有更小的节点了,浮动完毕,整棵树符合二叉堆规则。
以上就是删除节点的流程,下面我们用代码去实现。下面是加入了删除函数的 BinaryHeap类
using System;
public class BinaryHeap {
public Node root;
public void Insert(int data){
Node lastParentNode = TreeAlgo.FindParentOfFartestLeftLocation(root);
if(lastParentNode == null){
Console.WriteLine("Insert Root Node " + data);
root = new Node(data);
}else{
Node newNode = new Node(data);
if(lastParentNode.left == null){ // 如果左子树为空,则插入到左子树
lastParentNode.left = newNode;
} else if(lastParentNode.right == null){ // 如果右子树为空,则插入到右子树
lastParentNode.right = newNode;
}else{
Console.WriteLine("父节点错误,父节点左右子树都不为空,无法插入!");
return;
}
newNode.parent = lastParentNode;
Node opt = newNode;
// 以最小堆的方式插入节点,即父节点小于等于子节点
// 如果是以最大堆的方式插入,则父节点要大于等于子节点 只要将 <= 改为 >= 即可
while(opt != null && opt.parent != null && opt.data <= opt.parent.data){
int tmp = opt.data;
opt.data = opt.parent.data;
opt.parent.data = tmp;
opt = opt.parent;
}
}
}
public void Delete(int index){
// 1. 找到要删除的节点
Node optNode = TreeAlgo.GetIndexOfNodeWithLevelOrder(root, index);
// 2. 按层序遍历,找到最后一层最后一个节点
Node lastNode = TreeAlgo.GetLastNodeOfLevelOrder(root);
// 3. 使用最后一个节点的数据替换掉要删除节点的数据
optNode.data = lastNode.data;
// 4. 把最后一层最后一个节点删除掉
if(lastNode.parent.left == lastNode){
lastNode.parent.left = null;
}else if(lastNode.parent.right == lastNode){
lastNode.parent.right = null;
}
// 5. 要删除的节点数据已经被替换,现在需要根据数据浮动到正确的位置
// 首先要判断是往下浮动还是往上浮动,因为我们是按最小堆操作的,
// 所以要先判断当前节点是否比父节点 "小",如果是,则要往上浮动,反之往下浮动
if(optNode.parent != null && optNode.data < optNode.parent.data){
while(optNode.parent != null && optNode.data < optNode.parent.data){
int tmp = optNode.data;
optNode.data = optNode.parent.data;
optNode.parent.data = tmp;
optNode = optNode.parent;
}
}
else{
// 尝试往下浮动
while(optNode.left != null || optNode.right != null){
Node compareNode = null;
if(optNode.left != null && optNode.right != null){
if(optNode.left.data < optNode.right.data){
compareNode = optNode.left;
}else{
compareNode = optNode.right;
}
}
else{
if(optNode.left != null){
compareNode = optNode.left;
}else if(optNode.right != null){
compareNode = optNode.right;
}
}
// 往下浮动,交换数据
if(compareNode != null && optNode.data > compareNode.data){
int temp = optNode.data;
optNode.data = compareNode.data;
compareNode.data = temp;
}
optNode = compareNode;
}
}
}
}
上面的代码中,删除函数的参数传的是第几个节点。当然,你也可以改成删除某个特定值的节点,删除逻辑都是一样的。
下面是运行的代码
using System;
using System.Collections.Generic;
class Program
{
static void Main(string[] args)
{
BinaryHeap bh = new BinaryHeap();
bh.Insert(1);
bh.Insert(5);
bh.Insert(6);
bh.Insert(9);
bh.Insert(11);
bh.Insert(8);
bh.Insert(15);
bh.Insert(17);
bh.Insert(21);
TreeAlgo.LevelOrderTraversal(bh.root);
bh.Delete(1);
Console.WriteLine("------ Delete 1");
TreeAlgo.LevelOrderTraversal(bh.root);
}
}
以上就是二叉堆插入和删除的逻辑。