噪声函数与地图生成

在我学习声音信号处理的时候，我的大脑很自然地联想到了地图生成。这篇博客记录了关于信号处理的一些概念与地图生成相关的东西。这些知识点不是一些新的东西，但对我来说，是以前从未接触过的，所以我想记录一下，并且分享给大家。这篇博客会覆盖一些简单的主题，频率、振幅、噪声的种类、噪声的应用等。涉及到的数学部分，基本上只有正弦波形。

这里会从简单的概念开始，然后逐渐深入。

注意：下面涉及的代码，虽然是以 Python 来描述的（简单直观），但文章的目的是为了解释原理，使用任何语言都可以的。

1. 为什么随机性是有用的

我们在程序化的地图生成中要做的是生成一组输出，其中有一些东西是相同的，而有一些东西是不同的。例如，在我的世界这个游戏中，所有的地图都有很多相似性。生物群落，方块大小，生物群落的平均大小，洞穴的平均高度，不同石头所占的比例等等。但是，也有一些不同的地的：群落的位置，黄金的位置，洞穴的大小等等。作为游戏的设计者，需要决定哪些部分需要是相同的，哪些部分需要是不同的。

对于不同的部分，通常是使用随机数生成器。让我们来做一个极其简单的地图生成器：它将包含20个格子，其中某些格子将包含宝箱。结果如下请注意这个地图有多少共同的地方：首先它都是由格子组成（每个点作为一个格子），每行有20个格子，然后有两种类型的块，一个是空白，一个是宝箱。

但有一点是不同的，哪一个格子是什么类型，也就是说宝箱可能出现在从0到19的任何一个格子。

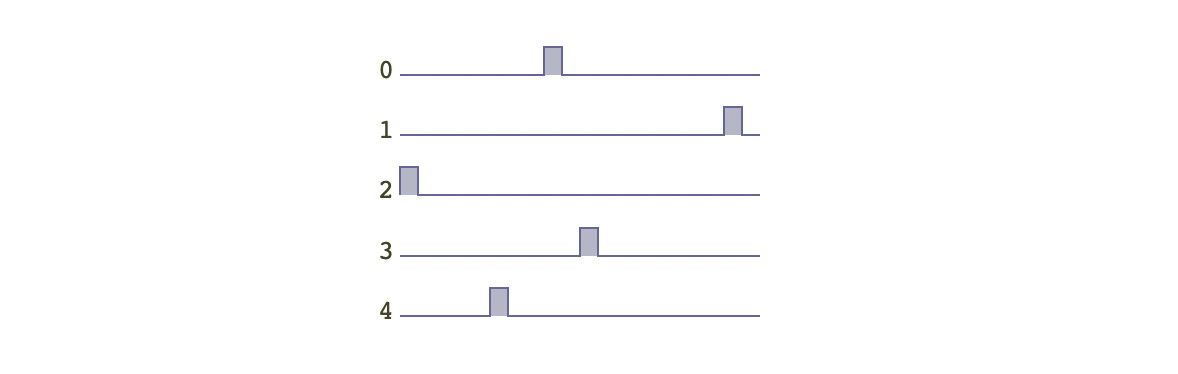
我们可以使用随机数来选择将宝箱放在哪一个格子中。最简单的方式是选择从0到19的随机数。这意味着每一个格子都可能被选择。大部分的编程语言都包含随机数生成函数。在 Python 中，使用方式是 random.randint(0, 19)。完整代码如下

def gen()
	map = [0] * 20
	pos = random.randint(0, 19)
	map[pos] = 1
	return map

for i in range(5):
	print_chart(i, gen())

生成结果如下：

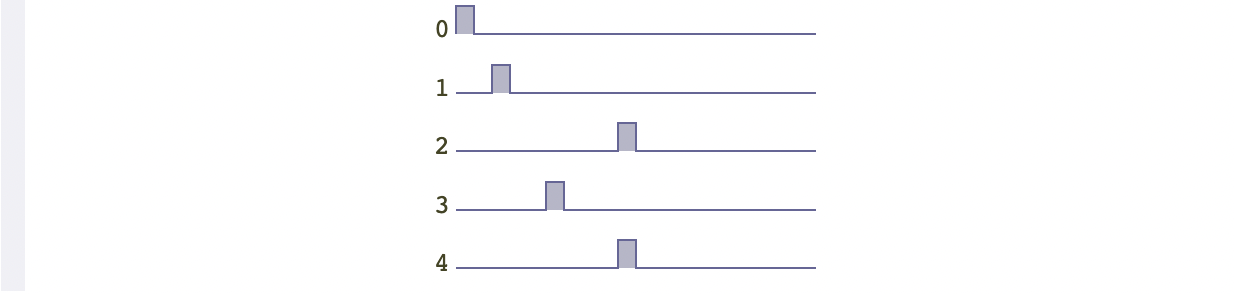
假设我们想让地图中的宝箱有更多的可能性出现在左边，这时就要使用非均匀随机数选择了。有很多方法可以完成这件事情，其中一种方式是首先选择一个随机数，然后将它向左移动，例如，使用函数 random(0,19)/2，下面是 Python 代码

def gen():
	map = [0] * 20
	pos = random.randint(0, 19) / 2
	map[pos] = 1
	return map

for i in range(5):
	print_chart(i, gen())

然后，如果我们想让宝箱更多地出现在左边，但是，右边也不能一个没有，应该怎么办呢？一个方式是使用平方数，也就是先选定一个随机数，然后计算它的平方，然后再用结果除以19(地图右边界索引)，得到的结果向下取整。下面是代码和效果

def gen():
	map = [0] * 20
	pos = random.randint(0, 19)
	pos = int(pos * pos / 19)
	map[pos] = 1
	return map

for i in range(1, 6):
	print_chart(i, gen())

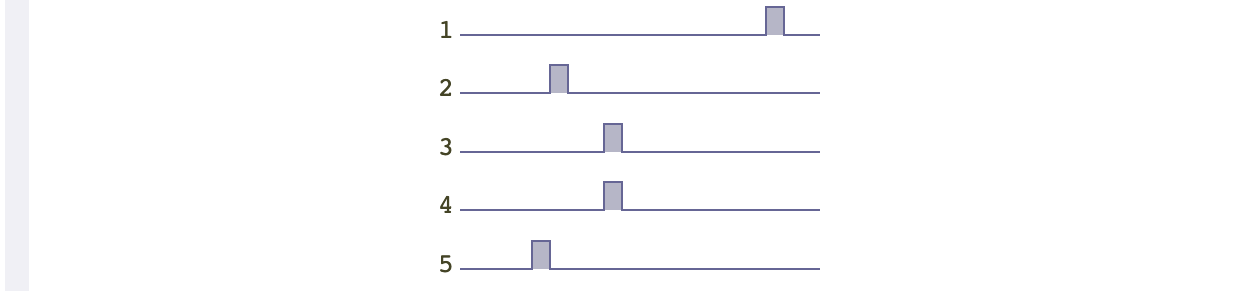
还有一种方法是使用两次随机。第一次先随机选择一个随机数，然后使用得到的这个随机数作为第二次随机的右边界。这样的结果就是假设我们第一次得到的随机数是19，那么最终宝箱的结果可能出现在地图的任何地方。但是，假设第一次得到的随机数是10，那么宝藏的位置，就有更多的可能性偏向左边。代码和效果如下

def gen():
	map = [0] * 20
	limit = random.randint(0, 19)
	pos = random.randint(0, limit)
	map[pos] = 1
	return map

for i in range(5):
	print_chart(i, gen())

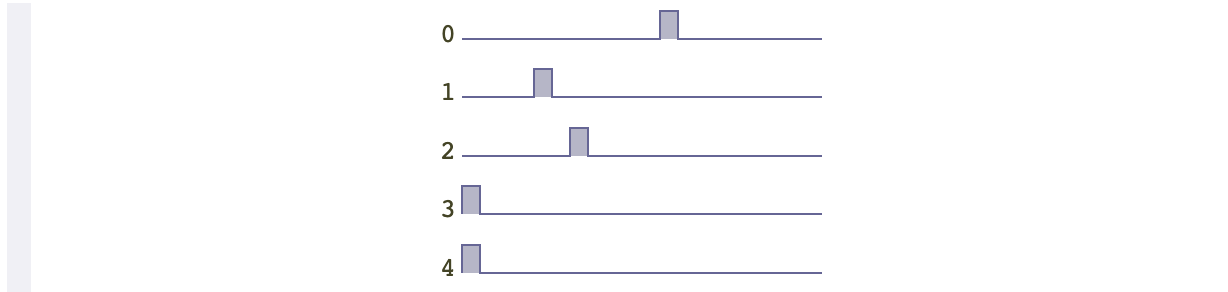
有很多方式可以将均匀随机数变为非均匀随机数。作为游戏设计者，我们需要根据自己的需求去选择合适的方式。

2. 什么是噪声

噪声是一系列的随机数，通常分布在一条线上或一个面上。

在以前老式的电视，如果一个电台没有信号，那么屏幕上就会显示很多黑白的噪点。对于收音机来说，如果没有信息，我们听到的可能就哧哧哧的声音，那也是噪声。

对于信号处理领域，噪声可理解为干扰正常信号的那些东西。例如在一个房间里有很多人说话，你很想听到特定的一个人在说什么，但是听不清，因为有其他人也在说话，那就是噪声。对于声音处理来说，这种噪声是分布在一条线上，也就是1D的。而在图片处理中，一个图片因为模糊或者很多噪点而看不清原本想要的画面，这种噪声是在一个面上，是一个2D的。当然，也可以有分布于3D，4D的噪声。

对于很多应用来说，我们尝试减少噪声。但对于自然界来说，很多东西看起来并不是纯粹的，而是充满了一部分噪声。所以，如果想让程序化生成的东西看起来更自然一些，我们需要添加噪声。噪声可以使程序化生成的东西看起来不一样，同时又具有一个基本的可识别结构。这个我们要根据具体的需要来看。

让我们来看一个使用噪声的例子。在之前，我们是在1D的地力上生成单个宝箱，现在我们想创造一个2D地图，由山谷，丘陵，和山脉组成。这里首先为每一个位置使用一个均匀的随机数选择，也就是 random(1,3)。我们定义1为山谷，2为丘陵，3为山脉。整个2D地图是存放在一个数组中，而每一个格子，存储了生成的随机数。下面是 Python 代码

for i in range(5):
	random.seed(i)
	print_chart(i, [random.randint(1,3) for i in range()])

这段 Python 代码看不懂也没关系，反正我也看不懂，但是最终其实就是对一个二维数组进行赋值

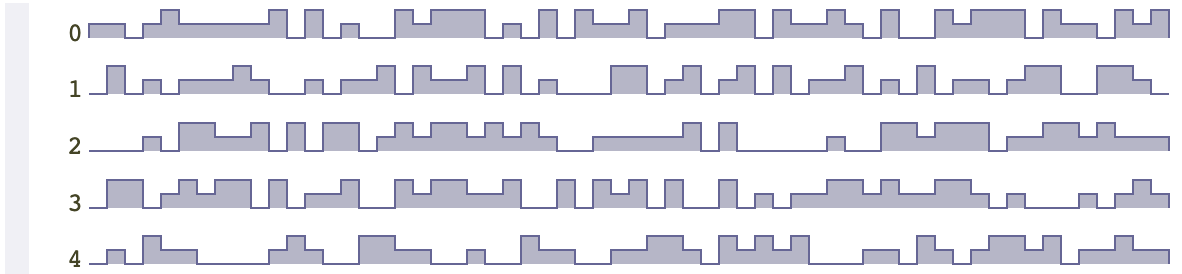
上面的结果看起来太随机了，有时候我们想要不那么均匀的随机，例如，山脉比丘陵更多一点，这种情况，就得使用非均匀随机

for i in range(5):
    random.seed(i)
    print_chart(i, [random.randint(1, random.randint(1, 3)) 
                    for i in range(mapsize)])

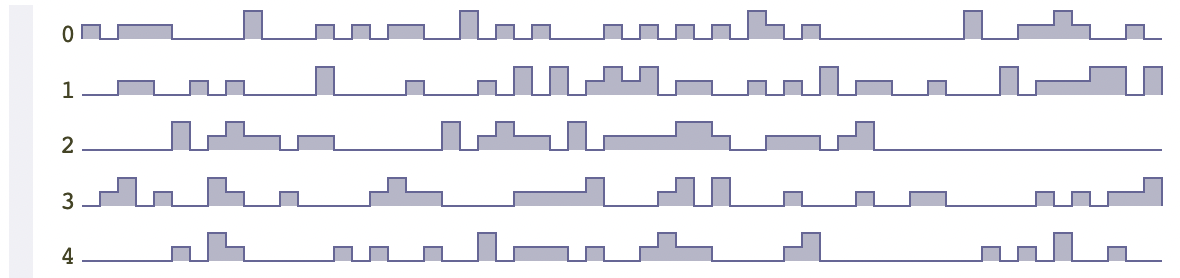
上面的非均匀随机对于我们想要的地图结果来说，并没有什么用，因为上面的随机是针对每一个位置，完全独立的随机，而我们想要的，是需要和周围的格子有一定关联的随机。

现在，该是噪声函数出场的时刻了。噪声函数生成的结果是一个序列，而不是随机函数那样，每次生成的是一个值。噪声函数的定义方式有很多，让我们先试一下最小值函数，也就是取邻近值中最小的那个值。假设原即噪声值数组为（1，5，2）。遍历原即数组，两两比较，取其中最小的时候，也就是先比较（1，5），取1，然后比较（5，2），取2，最终得到的序列为（1，2）。注意，这个噪声函数得到的最终序列元素个数，一定是比原即序列少1个的。将这个噪声函数应用于地图生成，代码如下

def adjacent_min(noise):
	output = []
	for i in range(len(noise) - 1):
		output.append(min(noise[i], noise[i + 1]))
	return output

for i in range(5):
	random.seed(i)
	noise = [random.randint(1, 3) for i in range(mapsize)]
	print_chart(i, adjacent_min(noise))

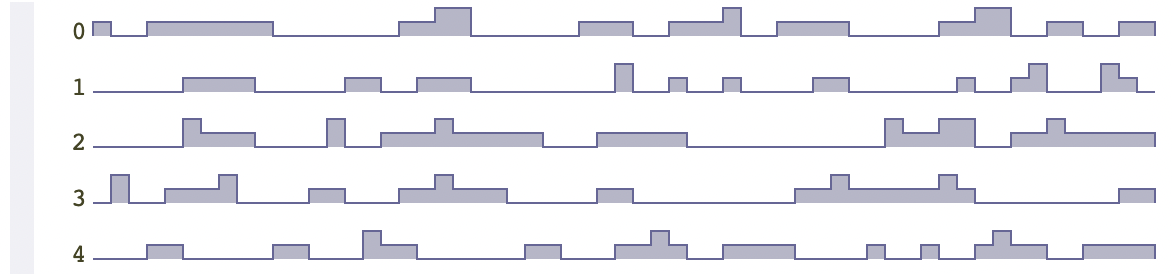
对比之前的生成结果，这个地图上的山谷、丘陵或山脉面积更大。山脉通常在丘陵附近。由于我们使用的噪声函数是最小值，所以山谷比山脉更常见。如果我们采用最大值，则山脉就会比山谷更常见。如果我们想让二者出现次数相当，可以采用平均数，而不是最小或最大值。上面的代码，每一次运行，都将生成不同的结果。

在程序化生成的过程中，通常做的就是尝试一下，看看结果是否OK，如果不OK，那就改一下代码，再尝试一下。

在信号处理中，平滑操作，也就是去掉不想要的噪声，叫做低通过滤器

回顾

噪声是一系列随机数的集合，通常是一维或二维的
在程序化生成中，我们通常添加噪声，以此让目标生成物变得不同
使用简单地生成随机数的方式创造噪声，会使每个元素与周围元素完全独立，不相关
我们通常希望噪声拥有一些特性，产生一定的模式
有很多生成噪声的方式
有一些噪声函数是直接生成噪声，而有一些是修改已有的噪声。

选择一个噪声函数有时候靠的是猜测，而了解噪声函数的原理以及如何修改，意味着可以做出更有根据的猜测。

3. 创造噪声

在之前的内容中，我们使用随机数作为输出，然后对其进行平滑。这一种常见的模式。对于一个随机函数，使用一组随机数作为参数，然后使用另一个随机数，来控制我们想要的内容，例如哪里是宝箱，哪里是山脉，哪里是山丘等等。

一些1D/2D的噪声生成器：

直接使用随机数作为输出。例如上面的山谷、山丘、山脉
使用随机数作为正弦和余弦的参数，这些参数用于输出
使用随机数作为梯度的参数，这些参数用于输出。这在Simplex/Perlin噪声中使用。

一些常用的修改噪声的方式：

应用一个过滤器来减少或放大某个特征。例如之前我们用平滑法来减少凹凸感，增加山谷的大小，并使山峰出现在山谷附近。
使用两个噪声函数来产生输出，通常会给每一个噪声函数赋予一个权重，以此来控制噪声函数对于输出结果的影响。
对于噪声函数产生的输出结果进行插值，来得到更加平滑的结果。

有很多方式可以创造噪声。从某种程度上来说，噪声如何产生，并不是很重要，但是将噪声用于游戏中，需要关注两件事情

你打算如何使用噪声
你希望从噪声函数中获得什么属性

4. 使用噪声的方式

使用噪声最直接的方式是作为海拔高度。在之前的例子中，我们使用 random(1,3) 来产生1、2、3这三个数，分别对应山谷、山丘、山脉。这是直接使用。

使用中点位移噪声或Simplex/Perlin噪声作为海拔，也是直接使用。

另一种使用噪声的方式是应用于移动中，简单来说就是下一步的移动，取决于上一步。例如一个噪声函数输出的值是 [2, -1, 5] 这可以表示为初始位置为2，然后移动，2 + -1 = 1，然后再移动 1 + 5 = 6，也就是最终走到了6的位置。

除了将噪声作为海拔高度外，还可能将它用于音频。

或者你要用它来做一个形状。例如，你可以在极坐标图中使用噪声作为半径。你可以把这样的一维噪声函数转换成极坐标形式，把输出作为半径而不是作为海拔。下面是同样的函数在极地形式下的样子。

或者你可能使用噪声作为图形纹理。Simplex/Perlin噪声经常被用于此。

你可以用噪音来选择物体的位置，如树木或金矿或火山或地震断层线。在前面的例子中，我用一个随机数来选择宝箱的位置。

你可以用噪声作为阈值函数。例如，你可以说，任何时候数值大于3，那么就会发生一件事，否则就会发生其他事情。这方面的一个例子是使用3D Simplex/Perlin噪声来生成洞穴。你可以说，任何高于某个密度阈值的东西都是不可行走的区域，任何低于该阈值的东西都是开放的空间（洞穴）。

5. 噪声的频率

频率是噪声的一个主要属性，最简单理解方式是直接看图，例如下面是正弦波的三种不同的频率，低频率，中频率，高频率的波形。

从上面三种不同的频率可以看出，低频率会使起伏更平缓，范围更大，则高频率会使起伏更尖锐。频率描述的是横向的属性。而振幅描述的是纵向的属性。在之前的例子中，山丘，山谷，山脉，看起来太过于『随机』了，意思就是我们需要更低一点的随机频率，来降低这种随机性，使其更加的缓和。

如果我们使用一个连续的噪声生成函数，增加频率，意味着输入参数的变化。而增加振幅，则意味着是对噪声函数产生的结果进行增量改变。假设噪声函数就是 sin(x)。增加频率，也就是 sin(x * 2) 则是两倍的频率。而增加振幅，则是 2 * sin(x)。

对于上面的图来说，改变的是频率，增大频率，意味着一个一个的波峰数量，频率越高，则两个波峰越多，两个波峰之间的距离越小。

对于上面的图来说，改变的是振幅，增加振幅，不会增加波峰的数量，而会改变波峰的高度。

上面的内容都是针对1D噪声的，对于2D噪声，也是同样的原理。

对于正弦波，我们还可以使用各种奇怪的组合，以此产生不同的效果。例如下面的这个例子，就是左边的频率更低一点，而右边的频率更高一点

通常来说，在同一时刻，可以使用多种不同频率的噪声，没有什么标准的规则，主要是看自己的需求，想要什么样的东西，然后再看怎么使用噪声。

6. 噪声的种类

不同种类的噪声拥有不同的频率。对于白噪声来说，所有的频率对于结果的贡献度，也可以说是权重，是一样的。例如我们前面的例子，使用1，2，3来代表山脉，山谷，丘陵。下面是条白噪声序列

在红色噪声，也称为布朗噪声中，低频会更加的突出。也就是说，会有更长的山谷和山丘。我们可以通过平均两个相邻随机数的形式，将白噪声变为布朗噪声。

def smoother(noise):
	output = []
	for i in range(len(noise) - 1):
		output.append(0.5 * (noise[i] + noise[i + 1]))
	return output

for i in range(8):
	random.seed(i)
	noise = [random.uniform(-1, +1) for i in range(mapsize)]
	print_chart(i, smoother(noise))

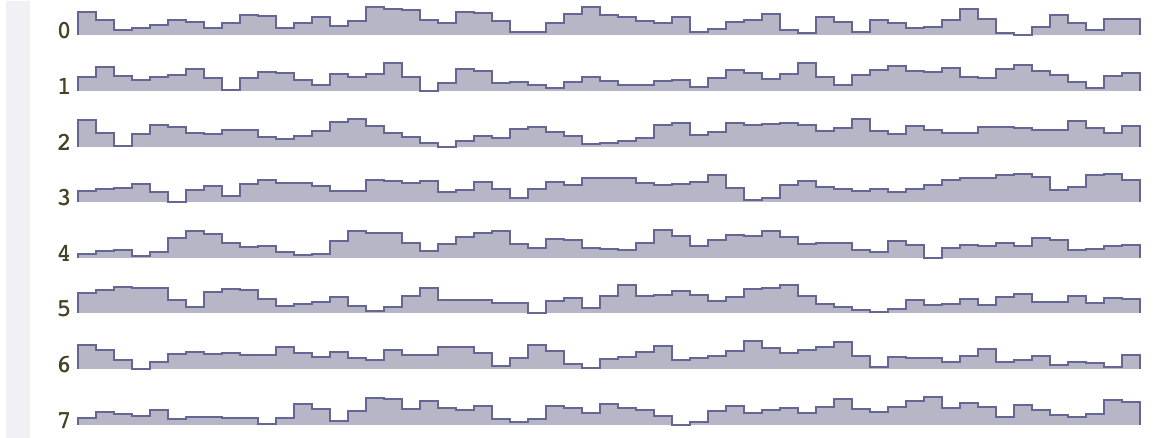
粉红噪声界于白噪声和布朗噪声之间，在自然界中也更常见。

在频谱的另一边，是蓝色噪声，高频会更加突出。我们可以使用白噪声中两个随机数之差，来产生蓝色噪声。

def rougher(noise):
	output = []
	for i in range(len(noise) - 1):
		output.append(0.5 * (noise[i] - noise[i + 1]))
	return output

for i in range(8):
	random.seed(i)
	noise = [random.uniform(-1, +1) for i in range(mapsize)]
	print_chart(i, rougher(noise))

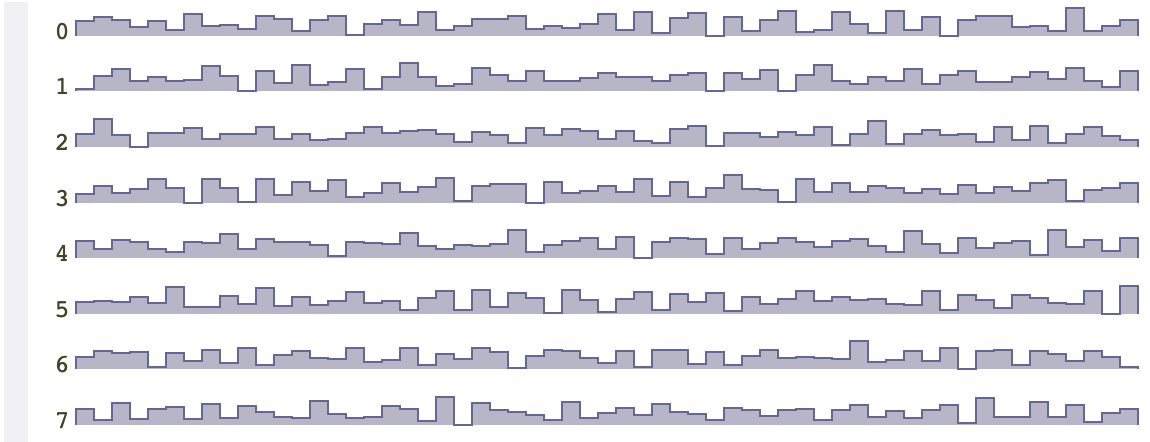
蓝色噪声可以用于地图中放置物体，它产生的结果不会很密集或者很稀疏，物体在地图中的分布整体比较均匀。

上面的内容我们已经了解了如何产生白噪声，布朗噪声，蓝色噪声，后面我们还会一起探究更多类型的噪声。

回顾

频率是一种重复的信号。
白噪声是最简单的，它是均匀地选择随机数。
红，粉，蓝等噪声在程序化生成中很有用。
将白噪声变为布朗噪声，可以使用相邻随机数的 + 操作
将白噪声变为蓝色噪声，可以使用相邻随机数的 - 操作

7. 组合频率

在之前的内容中我们了解了不同类型的噪声的特点。另一种生成噪声的方式是组合不同频率的噪声。例如，假设我们有一个噪声函数 noise ，会在特定的频率 freq 生成噪声。如果你想让 1000Hz 的噪声比 2000Hz 的噪声强一倍，并且没有其他频率的噪声，那么我们可以这样来生成 noise(1000) + 0.5 * noise(2000)

正弦函数看起来并不是很嘈杂，但是这个函数很容易给定一个频率，所以我先从正弦开始，然后一步一步往前走。

def noise(freq):
	phase = random.uniform(0, 2 * math.pi)
	return [math.sin(2 * math.pi * freq * x / mapsize + phase)
			for x in range(mapsize)]

for i in range(3):
	random.seed(i)
	print_chart(i, noise(1))

上面的结果，是把一个基础的正弦波使用一个随机量来控制其向侧面位移。这里唯一的随机性，是将它移的有多远。

接下来我们尝试将8个噪声函数加在一起，频率分别是 1，2，4，8，16，32。每一个噪声函数将乘以一个因子，可以理解为不同频率的权重。

def weighted_sum(amplitudes, noises):
	output = [0.0] * mapsize
	for k in range(len(noises)):
		for x in range(mapsize):
			output[x] += amplitudes[k] * noise[k][x]
	return output

amplitudes = [0.2, 0.5, 1.0, 0.7, 0.5, 0.4]
frequencies = [1,2,4,8,16,32]

for i in range(10):
	random.seed(i)
	noises = [noise(f) for f in frequencies]
	sum_of_noises = weighted_sum(amplitudes, noises)
	print_chart(i, sum_of_noises)

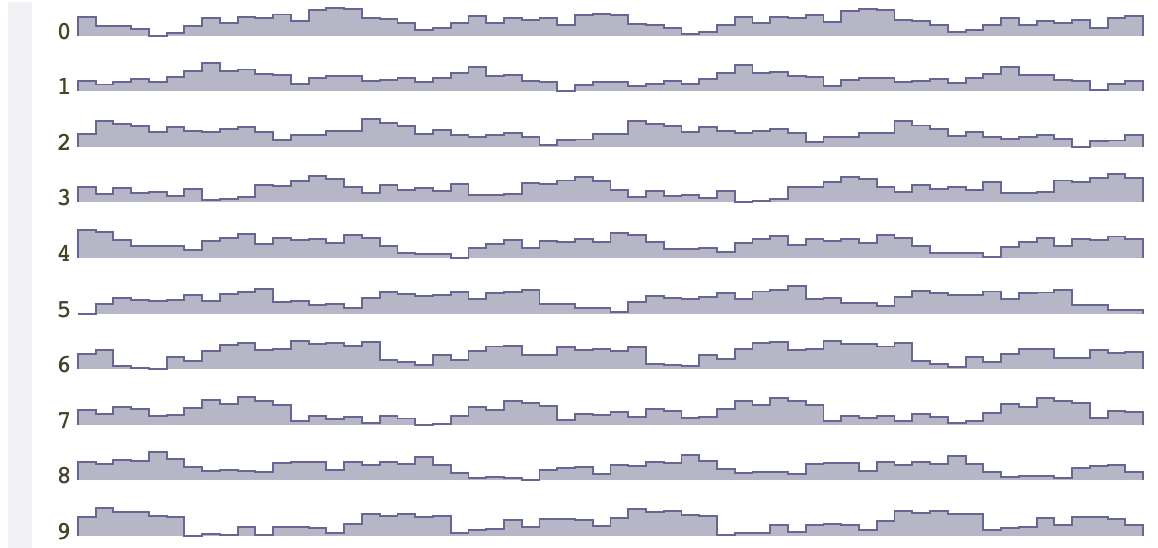
如果我们改变权重因子，也就是 amplitudes 数组，得到的结果就会不同。假设将 amplitudes 改为 [1.0, 0.7, 0.5, 0.3, 0.2, 0.1]，则得到的结果如下

而改为 [0.1, 0.1, 0.2, 0.3, 0.5, 1.0]，则结果如下

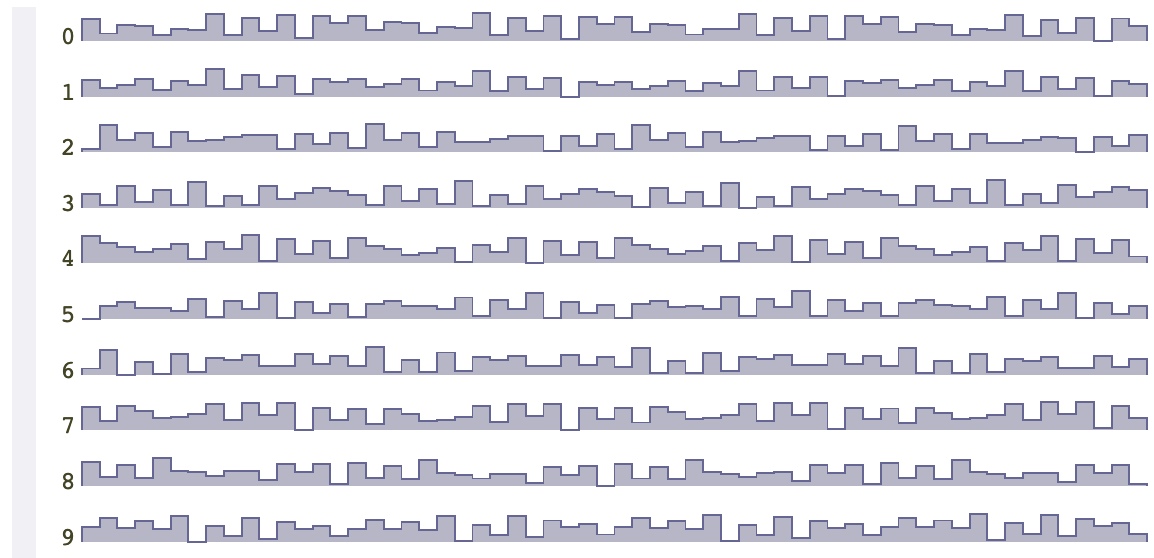
原文来自 https://www.redblobgames.com/articles/noise/introduction.html

1. 为什么随机性是有用的#

2. 什么是噪声#

回顾#

3. 创造噪声#

一些1D/2D的噪声生成器：#

一些常用的修改噪声的方式：#

4. 使用噪声的方式#

5. 噪声的频率#

6. 噪声的种类#

回顾#

7. 组合频率#