下面的公式有点多,只是把原教程中的公式详细展开了,一步一步来,很简单,相信我。
给定一个点,判断一个点是否在一个半径为 $R$ 的圆或者圆外、圆内,我们可以使用下面的公式来判断。这里假设圆心在 $(0,0,0)$ 点,半径为 $R$
如果一个点 $(x, y, z)$ 在圆上,则 $x^2 + y^2 + z^2 = R^2$
如果一个点 $(x, y, z)$ 在圆内,则 $x^2 + y^2 + z^2 < R^2$
如果一个点 $(x, y, z)$ 在圆外,则 $x^2 + y^2 + z^2 > R^2$
假设圆心在点 $C = (C_x, C_y, C_z)$,半径为 r,则根据上面的第一个公式,可以得到
$(x - C_x)^2 + (y - C_y)^2 + (z - C_z)^2 = r^2$
我们可以将点 $(x, y, z)$ 使用之前的 Vec3 向量表示,例如设 $点P = (x, y, z)$,则可以将上面的公式,换一种表达形式,也就是
$(P - C) \cdot (P - C) = r^2$
还记得我们的光线公式吗?$P(t) = A + tb$,A是光线的起点,b是光线的方向,t是一个缩放参数,而得到的 $P(t)$ 则是光线打到的点。我们想知道一条光线所打到的点,是否在圆上或者圆内。是不是只要将光线公式,代入上面的公式,就可以了?也就是将原来的点P,换成了光线函数 P(t),就会得到下面的公式
$(P(t) - C) \cdot (P(t) - C) = r^2$
由于 $P(t) = A + tb$,所以我们展开上面的公式,可以得到
$(A + tb - C) \cdot (A + tb - C) = r^2$
而上面的公式,又可以换成另一种表达形式
$(A + tb - C)^2 = r^2$
这个公式就是我们以前很熟悉的 $(a + b - c)^2$ 的形式,展开形式就是 $a^2 + 2ab - 2ac + b^2 - 2bc + c^2$
那么,我们将公式 $(A + tb - C)^2 = r^2$ 用同样的方式展开,则可以得到
$A^2 + 2Atb - 2AC + (tb)^2 - 2tbC + C^2 = r^2$
整理一下,我们可以看出,上面的第1项、第3项、第6项,可以组合到一起组成一个公式,也就是 $A^2 - 2AC + C^2 = (A - C) \cdot (A - C)$,修改上面的式子,可以得到
$2Atb + (tb)^2 - 2tbC + (A - C) \cdot (A - C) = r^2$
上面的式子中 $2Atb$ 和 $2tbC$ 都有一个 $2tb$,可以组合一下,得到 $2tb \cdot (A - C)$,用这种形式修改上面的公式,得到
$(tb)^2 + 2tb \cdot (A - C) + (A - C) \cdot (A - C) = r^2$
而 $(tb)^2$ 可以换成一种形式,表示成 $t^2 \cdot b^2$,再换一种形式可以为 $t^2b \cdot b$,用这种形式修改上面的公式,可以得到最终的公式如下
$t^2b \cdot b + 2tb \cdot (A - C) + (A - C) \cdot (A - C) = r^2$
将 $r^2$ 移到公式左边,可以得到
$t^2b \cdot b + 2tb \cdot (A - C) + (A - C) \cdot (A - C) - r^2 = 0$
这就是最终的公式了,为什么要绕这么多换成这样一个形式呢,我猜作者是为了计算方便,写代码方便。
对于上面的公式,我们已经知道 A 是光线的起点,C 是圆心,而 b 是光线的方向,r 是圆的半径,唯一不知道的变量就是 t,而上面的方程,是一个一元二次方程,根据上学时学的知识,我们知道一元二次方程的解,可能有0个,1个,或2个。对于上面公式,也就是我们渲染圆的目标而已,只要有 > 0 个解,则说明光线打到了圆。
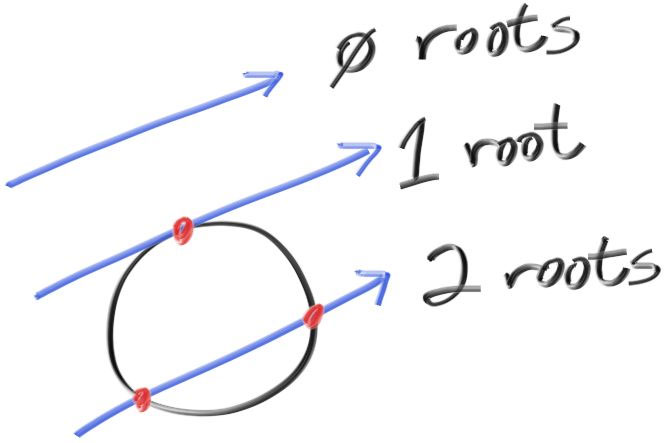
接下来还没完,我们如何知道上面的公式解的个数呢?根据一元二次方程的形式
$ax^2 + bx + c = 0$
它的根可以表示为 $\frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$
对于上面公式中的 $b^2 - 4ac$,如果结果大于 0,则方程有两个不相等的实数根,等于 0,则方程有两个相等的实数根,小于 0,则方程无实数根。
所以,我们只需要将之前的公式
$t^2b \cdot b + 2tb \cdot (A - C) + (A - C) \cdot (A - C) - r^2 = 0$
表示成
$ax^2 + bx + c = 0$ 的形式,则可以很方便的知道方程有几个解。
对于我们而言,上面的公式,除了 $t$ 之外,其他的变量都是已知道的,我们直接在代码中去转换。这次的代码沿用上一小节的,然后在 main.rs 中添加一个函数 hit_sphere
fn hit_sphere(center: Vec3, radius: f64, r: Ray) -> bool {
// 公式中的 (A - C)
let oc = r.origin - center;
// 公式中第1项的 b*b
let a = Vec3::dot(r.direction, r.direction);
// 公式中第2项的内容,忽略 t
let b = 2.0 * Vec3::dot(oc, r.direction);
// 公式中的 (A - C) * (A - C) - r^2
let c = Vec3::dot(oc, oc) - radius * radius;
// 计算出了 a, b, c,判断 b^2 - 4ac 解的个数
let result = b * b - 4.0 * a * c;
// 解的个数 >= 0,则打到了圆
return result >= 0.0;
}
然后在 ray_color 函数中添加是否打到圆的判断,如果打到了圆,我们就返回当前像素为红色
fn ray_color(r: Ray) -> Color {
if hit_sphere(Vec3::new(0.0, 0.0, -1.0), 0.5, r) {
return Color::new(1.0, 0.0, 0.0);
}
// 将光线的方向标准化,保证其值在 -1 到 1 之间
let unit_direction = Vec3::unit_vector(r.direction);
// 为了计算方便,我们将方向的 y 值,从 [-1,1] 映射到 [0, 1]
let t = 0.5 * (unit_direction.y + 1.0);
// 做一个蓝白渐变,当 t 为 0 时,就是白色,将 t 为 1 时,就是蓝色
return (1.0 - t) * Color::one() + t * Color::new(0.5, 0.7, 1.0);
}
cargo run > sphere.ppm 最终效果图如下
