法线的定义是垂直于面的向量。对于一个球体来说,法线的向量,就是球上某个点,减去球心坐标,所得到的向量。
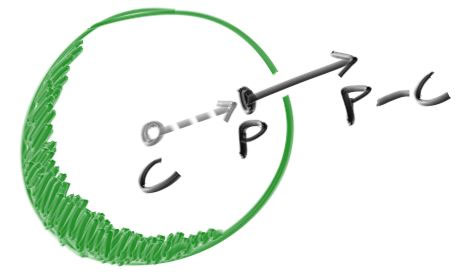
虽然法线向量看不到,但是我们可以将它的值,使用 RGB 颜色值的形式,显示出来,这样我们可以有一个大概的视觉上的了解。最终的效果图如下

在前一小节,我们只知道光线是否打到了球了,而现在要求法向量,我们就需要知道光线打到球的哪个位置。而一条光线打到球,可能有两个点,这里,我们先只取最近那个点的坐标。代码如下,在上一节代码的修改了 hit_sphere 函数和 ray_color 函数
//src main.rs
fn hit_sphere(center: Vec3, radius: f64, r: Ray) -> f64 {
// 公式中的 (A - C)
let oc = r.origin - center;
// 公式中第1项的 b*b
let a = Vec3::dot(r.direction, r.direction);
// 公式中第2项的内容,忽略 t
let b = 2.0 * Vec3::dot(oc, r.direction);
// 公式中的 (A - C) * (A - C) - r^2
let c = Vec3::dot(oc, oc) - radius * radius;
// 计算出了 a, b, c,判断 b^2 - 4ac 解的个数
let result = b * b - 4.0 * a * c;
// -----------------------------------
if result < 0.0 {
return -1.0;
} else {
return (-b - result.sqrt()) / (2.0 * a);
}
// -----------------------------------
}
fn ray_color(r: Ray) -> Color {
// -----------------------------------
let t = hit_sphere(Vec3::new(0.0, 0.0, -1.0), 0.5, r);
if t > 0.0 {
let unit_normal = Vec3::unit_vector(r.at(t) - Vec3::new(0.0, 0.0, -1.0));
return 0.5
* Color::new(
unit_normal.x + 1.0,
unit_normal.y + 1.0,
unit_normal.z + 1.0,
);
}
// -----------------------------------
// 将光线的方向标准化,保证其值在 -1 到 1 之间
let unit_direction = Vec3::unit_vector(r.direction);
// 为了计算方便,我们将方向的 y 值,从 [-1,1] 映射到 [0, 1]
let t = 0.5 * (unit_direction.y + 1.0);
// 做一个蓝白渐变,当 t 为 0 时,就是白色,将 t 为 1 时,就是蓝色
return (1.0 - t) * Color::one() + t * Color::new(0.5, 0.7, 1.0);
}
ray_color 函数中拿到 hit_sphere 函数返回的结果 t,然后通过 t 和光线的原点及方向,来计算出打到的位置,通过光线打到的位置,减去球心的坐标,就可以得出法向量,然后将法向量进行标准化,得到值 (x, y, z) 值在 -1 到 1 之间。
乘 0.5 和 加 1 的意思是将 -1 到 1 的值,映射到 0 到 1 之间,然后就可以将这个值作为颜色值来显示(着色)了。