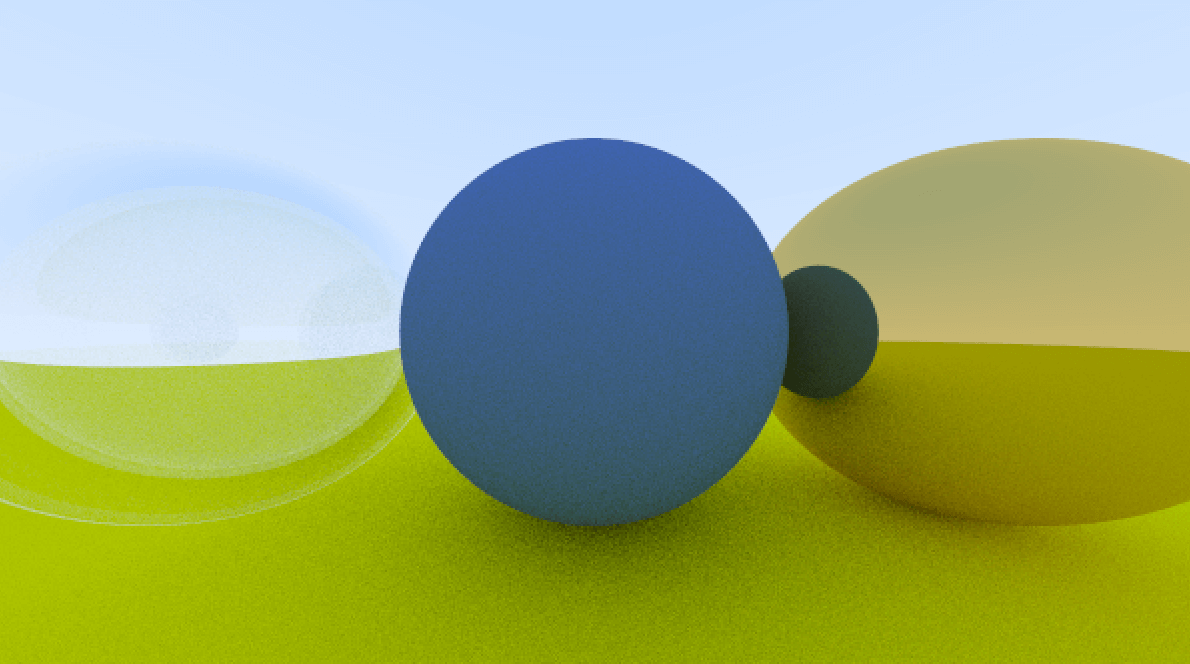关于折射的实现,可以使用斯涅尔定律。当光波从一种介质传播到另一种介质时,如果两种介质拥有不同的折射率,那么光线就会发生折射现象。例如光线从空气中进入水中,或者从空气中进入玻璃中。
下面涉及到的公式,也可以不用理解推导过程,只要拿来用就行。
斯涅尔定律
斯涅尔定律表明,当光波从介质1传播到介质2时,假若两种介质的折射率不同,则会发生折射现象,其入射光和折射光都处于同一平面,称为“入射平面”,并且与界面法线的夹角满足如下关系:
$n_{1}\sin\theta_{1} = n_{2}\sin\theta_{2}$
其中,$n_{1}$、$n_{3}$ 分别是两种介质的折射率,$\theta_{1}$、$\theta_{2}$ 分别是入射光线、折射光线与界面法线的夹角,分别叫做入射角和折射角。
要求折射光线的方向,就需要解出 $\sin\theta_{2}$ 来。根据上面的公式可知
$\sin\theta_{2} = \frac{n_{1}}{n_{2}} \cdot \sin\theta_{1}$
我们可以将折射光线的向量,分解为一个垂直向量和一个平行向量。计算出这两个向量,然后相加,即可得到最终的折射向量。
$ 垂直向量 = \frac{n_{1}}{n_{2}}(入射向量 + \cos\theta_{1}*法向量)$
$ 平行向量 = - \sqrt{1 - |垂直向量|^2 * 法向量}$
由于,两个向量的点乘与其夹角的 cos 值有关,也就是 $ a \cdot b = |a||b|\cos\theta $ ,如果 a 和 b 都是单位向量,那么可得到 $a \cdot b = \cos\theta$
根据上面的规则,可以使用新的方式来表示垂直向量
$ 垂直向量 = \frac{n_{1}}{n_{2}}(入射向量 + (-入射向量 \cdot 法向量) * 法向量) $
综上,可以使用代码来实现折射逻辑,在 vec3.rs 中添加一个新的函数 refract
// src/vec3.rs
pub fn refract(unit_in_v: Vec3, n: Vec3, etai_over_etat: f64) -> Vec3 {
let cos_theta = Vec3::dot(-unit_in_v, n).min(1.0);
let r_out_perp = etai_over_etat * (unit_in_v + cos_theta * n);
let r_out_parallel = -((1.0 - r_out_perp.length_squared()).abs().sqrt()) * n;
return r_out_perp + r_out_parallel;
}
然后添加 Dielectric 材质
// src/material.rs
pub struct Dielectric {
pub ir: f64, // 不同介质的折射率
}
impl Dielectric {
pub fn new(ir: f64) -> Self {
Self { ir }
}
}
impl Material for Dielectric {
fn scatter(&self, r_in: &Ray, hit_record: &HitRecord) -> Option<(Ray, Color)> {
let attenuation = Color::one();
let refraction_ratio = if hit_record.front_face {
1.0 / self.ir
} else {
self.ir
};
let unit_in_direction = Vec3::unit_vector(r_in.direction);
let refracted = Vec3::refract(unit_in_direction, hit_record.normal, refraction_ratio);
let scattered = Ray::new(hit_record.p, refracted);
return Some((scattered, attenuation));
}
}
然后修改 main 函数中的 material_center 和 material_left 材质
// src/main.rs
let material_center = Dielectric::new(1.5);
let material_left = Dielectric::new(1.5);
使用 cargo run --release > refracts.ppm 可以得到下面的图
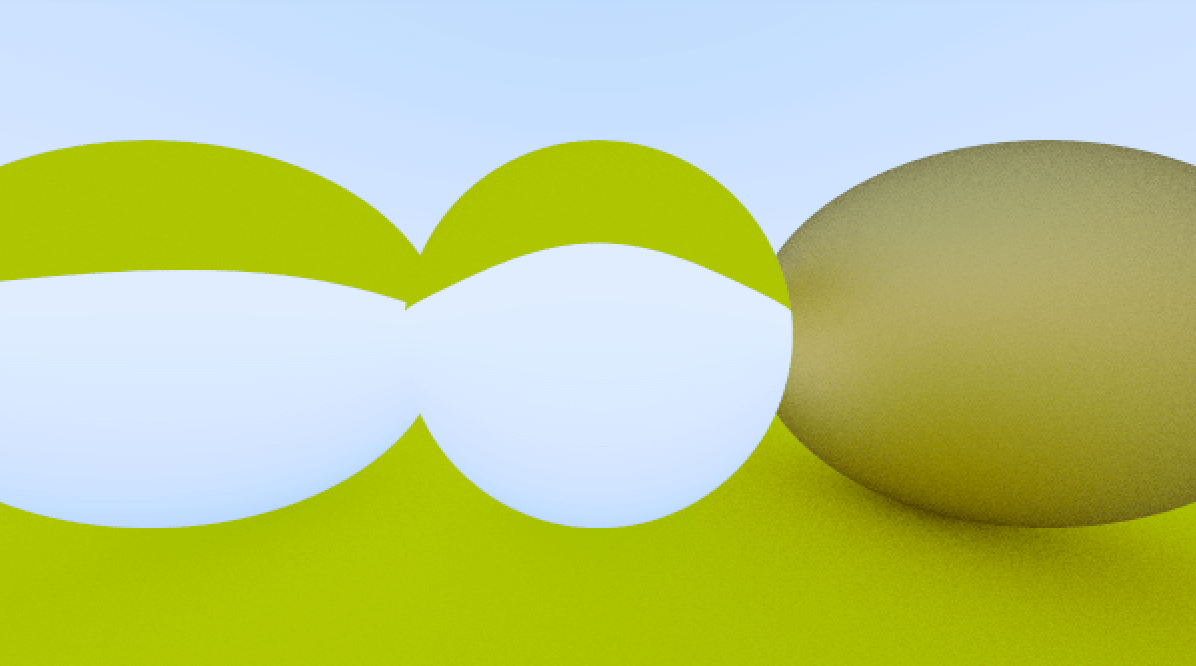
全内反射与临界角
假设光线从折射率较大的价质传播进入折射率较小的价质,则入射角越大,光线的折射角也越大,直至当入射角大于临界角时,由于折射角不能大于90度,这时会出现全内反射。
由于 $ \sin\theta_{2} = \frac{n_{1}}{n_{2}} \cdot \sin\theta_{1} $,假设 $n_{1} = 1.5,n_{2} = 1.0 $ 也就是 $\sin\theta_{2} = \frac{1.5}{1.0} \cdot \sin\theta_{1}$。由于 $\sin\theta_{2}$ 的值不能大于 1.0,所以如果 $\frac{1.5}{1.0} \cdot \sin\theta_{1} > 1.0$ 则会发生全内反射。
根据三角函数可以求出 $\sin\theta_{1}$ 的值。$\sin\theta_{1} = \sqrt{1 - \cos^2\theta_{1}} $。
而 $\cos\theta_{1} = 入射向量 \cdot 法向量$
修改 Dielectric 材质的代码,将全内反射的逻辑添加进去。
// src/material.rs
impl Material for Dielectric {
fn scatter(&self, r_in: &Ray, hit_record: &HitRecord) -> Option<(Ray, Color)> {
let attenuation = Color::one();
let refraction_ratio = if hit_record.front_face {
1.0 / self.ir
} else {
self.ir
};
let unit_in_direction = Vec3::unit_vector(r_in.direction);
let cos_theta = Vec3::dot(-unit_in_direction, hit_record.normal).min(1.0);
let sin_theta = (1.0 - cos_theta * cos_theta).sqrt();
let cannot_refract = refraction_ratio * sin_theta > 1.0;
let direction = if cannot_refract {
Vec3::reflect(unit_in_direction, hit_record.normal)
} else {
Vec3::refract(unit_in_direction, hit_record.normal, refraction_ratio)
};
let scattered = Ray::new(hit_record.p, direction);
return Some((scattered, attenuation));
}
}
修改 main 函数中的材质代码,将四个材质的代码修改如下
// src/main.rs
let material_ground = Lambertian::new(Color::new(0.8, 0.8, 0.0));
let material_center = Lambertian::new(Color::new(0.1, 0.2, 0.5));
let material_left = Dielectric::new(1.5);
let material_right = Metal::new(Color::new(0.8, 0.6, 0.2), 0.0);
使用 cargo run --release > dielectric_and_shinny_sphere.ppm 可以得到下面的图

Schlick 近似
现实世界中,不同的角度,会导致不同的反射率,以陡峭的角度看玻璃,它会产生镜子的特性。对于这一点的实现比较复杂,但是大家都会使用一种简单并且能达到近似效果的方法,也就是 Schlick 近似,具体的原理,请查看 Wiki,我们直接修改代码,添加逻辑。
在 Dielectric 的实现中,添加一个函数 reflectance
// src/material.rs
impl Dielectric {
pub fn new(ir: f64) -> Self {
Self { ir }
}
pub fn reflectance(cosine: f64, ref_idx: f64) -> f64 {
let mut r0 = (1.0 - ref_idx) / (1.0 + ref_idx);
r0 = r0 * r0;
return r0 + (1.0 - r0) * (1.0 - cosine).powf(5.0);
}
}
然后修改 Dielectric 的 Material Trait 的实现
// src/material.rs
impl Material for Dielectric {
fn scatter(&self, r_in: &Ray, hit_record: &HitRecord) -> Option<(Ray, Color)> {
let attenuation = Color::one();
let refraction_ratio = if hit_record.front_face {
1.0 / self.ir
} else {
self.ir
};
let unit_in_direction = Vec3::unit_vector(r_in.direction);
let cos_theta = Vec3::dot(-unit_in_direction, hit_record.normal).min(1.0);
let sin_theta = (1.0 - cos_theta * cos_theta).sqrt();
let cannot_refract = refraction_ratio * sin_theta > 1.0;
let mut rng = rand::thread_rng();
let random_double = rng.gen();
let direction = if cannot_refract
|| Dielectric::reflectance(cos_theta, refraction_ratio) > random_double
{
Vec3::reflect(unit_in_direction, hit_record.normal)
} else {
Vec3::refract(unit_in_direction, hit_record.normal, refraction_ratio)
};
let scattered = Ray::new(hit_record.p, direction);
return Some((scattered, attenuation));
}
}
通过上面的修改,我们可以实现一个空心玻璃球效果,修改 main 函数,添加一个新的材质和一个新的球体。这个球体的半径为负的,而对于它的几何形状没有影响,但是这将使它的法线向内,最终形成一个空心玻璃球效果。
// main.rs
let material_left2 = Dielectric::new(1.5);
world.add(Box::new(Sphere::new(
Vec3::new(-1.0, 0.0, -1.0),
-0.4,
material_left2,
)));
使用 cargo run --release > hollow_glass_sphere.ppm 可以得到下面的图