上一篇博客我们实现了一些简单的数学曲面,这一节我们将继续更复杂的数学曲面展示,所有资源完全承接上一篇内容。
2.5 创建一个涟漪效果
先来看一下最终要实现的效果图
我们一步一步来实现这个效果。首先,要创建一个基于到原点距离正弦波。而这个距离,我们使用毕达哥拉斯定理也就是勾股定理 $a^2 + b^2 = c^2$ 。对于这个效果来说,我们是基于XZ坐标来求Y坐标的,所以也就是 $\sqrt{x^2 + z^2}$ 。
在 Graph.cs 中添加一个新函数 Ripple,然后使用 Mathf.Sqrt 来计算距离。
public static float Ripple(float x, float z, float t)
{
float d = Mathf.Sqrt(x * x + z * z);
float y = d;
return y;
}
然后别忘记将函数添加到数组中,名字添加到枚举中
static GraphFunction[] functions =
{
SineFunction,
MultiSineFunction,
Sine2DFunction,
MultiSine2DFunction,
Ripple,
};
public enum GraphFunctionName
{
Sine,
MultiSine,
Sine2D,
MultiSine2D,
Ripple,
}
当前运行后效果图如下
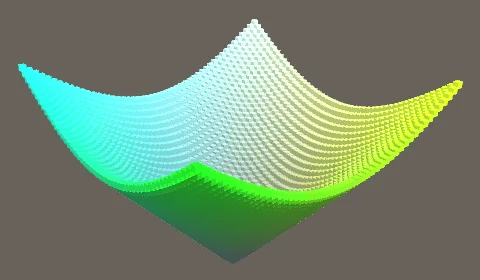
现在我们拥有了一个静态的圆锥体形状,要创建波纹,我们要使用 $f(x,z,t) = sin(πD)$,这里的 D 就是距离。
float d = Mathf.Sqrt(x * x + z * z);
float y = Mathf.Sin(pi * d);
return y;
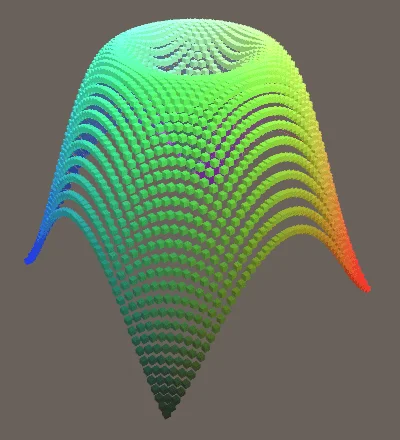
目前的结果并没有显示出太多的波形,所以我们提高频率
float y = Mathf.Sin(4f * pi * d);

现在的形状已经开始接近最终目标效果,但是波动的幅度有点太极端了。我们要以通过降低振幅来调整图形的形状,但是由于我们的波形是依赖于距离的,所以我们直接调整距离即可。例如使用 $\frac{1}{10D}$,为了避免因为距离为0而导致的除0错误,我们使用 $\frac{1}{1 + 10D}$
public static float Ripple(float x, float z, float t)
{
float d = Mathf.Sqrt(x * x + z * z);
float y = Mathf.Sin(4f * pi * d);
y /= 1f + 10f * d;
return y;
}

现在的效果已经和最终的效果很像了对不对,接下来只需要将时间变量加上即可拥有动画效果。
public static float Ripple(float x, float z, float t)
{
float d = Mathf.Sqrt(x * x + z * z);
float y = Mathf.Sin(pi * (4f * d - t));
y /= 1f + 10f * d;
return y;
}
运行看效果。
3 从一维到三维
在此之前的代码中,我们都是通过X和Z去定义Y,这样可以表现出很多效果,但是,限制太大。所以我们接下来要修改之前的函数,使输出单一的 float 变为输出 Vector3。
3.1 三维函数
如果我们的函数改为输出 Vector3,这将允许我们创建任意的曲面。
例如,函数 $f(x,z) = \begin{bmatrix} x \\ 0 \\ z \end{bmatrix}$ 用来描述XZ平面。而函数 $f(x,z) = \begin{bmatrix} x \\ z \\ 0 \end{bmatrix}$ 用来描述XY平面。
由于参数的输入值,并不一定是 X 和 Z,所以这里用用 x 和 z 来作为参数名就不太合适了,所以我们改为使用 u 和 v。函数就像 $f(u,v) = \begin{bmatrix} u + v \\ uv \\ \frac{u}{v} \end{bmatrix}$ 这样。
接下来统一修改一下我们之前的代码。
首先修改 GraphFunction 的委托定义代码,将返回值类型改为 Vector3,形参名改为 u v。
public delegate Vector3 GraphFunction(float u, float v, float t);
接下来修改各个函数,对于Sine函数来说,它所要表现的公式已经变为 $f(u,v,t) = \begin{bmatrix} u \\ sin(π(u + t)) \\ v \end{bmatrix}$。
修改我们已有的函数代码如下
public static Vector3 SineFunction(float x, float z, float t)
{
float y = Mathf.Sin(pi * (x + t));
Vector3 p = new Vector3(x, y, z);
return p;
}
public static Vector3 MultiSineFunction(float x, float z, float t)
{
float y = Mathf.Sin(pi * (x + t));
y += Mathf.Sin(2f * pi * (x + 2f * t)) / 2f;
y *= 2f / 3f;
Vector3 p = new Vector3(x, y, z);
return p;
}
public static Vector3 Sine2DFunction(float x, float z, float t)
{
float y = Mathf.Sin(pi * (x + t));
y += Mathf.Sin(pi * (z + t));
y *= 0.5f;
Vector3 p = new Vector3(x, y, z);
return p;
}
public static Vector3 MultiSine2DFunction(float x, float z, float t)
{
float y = 4f * Mathf.Sin(pi * x + z + t * 0.5f);
y += Mathf.Sin(pi * (x + t));
y += Mathf.Sin(2f * pi * (z + 2f * t)) * 0.5f;
y *= 1f / 5.5f;
Vector3 p = new Vector3(x, y, z);
return p;
}
public static Vector3 Ripple(float x, float z, float t)
{
float d = Mathf.Sqrt(x * x + z * z);
float y = Mathf.Sin(pi * (4f * d - t));
y /= 1f + 10f * d;
Vector3 p = new Vector3(x, y, z);
return p;
}
修改 Update 函数的代码如下
void Update()
{
float t = Time.time;
GraphFunction f = functions[(int)function];
float step = 2f / resolution;
for(int i = 0, z = 0; z < resolution; ++z)
{
float v = (z + 0.5f) * step - 1f;
for(int x = 0; x < resolution; ++x, ++i)
{
float u = (x + 0.5f) * step - 1f;
points[i].localPosition = f(u, v, t);
}
}
}
在初始化的时候,其实并不需要关心每一个点的位置,因为会在 Update 时重新计算,所以可以简化 Awake 函数,代码如下
void Awake()
{
float step = 2f / resolution;
Vector3 scale = Vector3.one * step;
points = new Transform[resolution * resolution];
for(int i = 0; i < points.Length; ++i)
{
Transform point = Instantiate(pointPrefab);
point.localScale = scale;
point.SetParent(transform, false);
points[i] = point;
}
}
3.2 创建一个圆柱体
为了证明我们已经可以不限于点的(X,Z)坐标,所以接下来我们创建一个圆柱体,以及动画。
还是老路子,先添加一个函数 Cylinder,不要忘记加到函数数组以及枚举中。
public static Vector3 Cylinder (float u, float v, float t)
{
Vector3 p;
p.x = 0f;
p.y = 0f;
p.z = 0f;
return p;
}
一个圆柱体,首先得是一个圆形的,对于一个圆来说,所有的点可以被定义为 $\begin{bmatrix} sin(θ) \\ cos(θ) \end{bmatrix}$,而θ的值是从0到2π。我们这里使用 u 来代替 θ。所以,在我们的例子中,创建一个XZ平面的圆,公式就变为了 $f(u) = \begin{bmatrix} sin(πu) \\ 0 \\ cos(πu) \end{bmatrix}$。代码如下
public static Vector3 Cylinder (float u, float v, float t)
{
Vector3 p;
p.x = Mathf.Sin(pi * u);
p.y = 0f;
p.z = Mathf.Cos(pi * u);
return p;
}
当前的运行效果如下

接下来,使y值等于v,这样我们就可以通过向上堆叠平面圆,而创造出一个圆柱
public static Vector3 Cylinder (float u, float v, float t)
{
Vector3 p;
p.x = Mathf.Sin(pi * u);
p.y = v;
p.z = Mathf.Cos(pi * u);
return p;
}

在此之前,我们是以单位圆为基础,来创造圆柱的。其实可以通过一个权值R,来修改圆柱的直径,也就是x和z的值,来达到更多的效果,所以函数就变为了 $f(u,v) = \begin{bmatrix} Rsin(πu) \\ v \\ Rcos(πu) \end{bmatrix}$
public static Vector3 Cylinder (float u, float v, float t)
{
Vector3 p;
float r = 1f;
p.x = r * Mathf.Sin(pi * u);
p.y = v;
p.z = r * Mathf.Cos(pi * u);
return p;
}
通过修改 R 值,可以造成不同的效果,例如 $R = 1 + \frac{sin(6πu)}{5}$
float r = 1f + Mathf.Sin(6f * pi * u) * 0.2f;

我们也可以让 R 值 依赖说 v,例如 $R = 1 + \frac{sin(2πv)}{5}$
float r = 1f + Mathf.Sin(2f * pi * v) * 0.2f;

也可以同时使用 u 和 v 来创建一个倾斜的波浪,同时加上时间参数t,就可以有动画效果。
float r = 0.8f + Mathf.Sin(pi * (6f * u + 2f * v + t)) * 0.2f;
3.3 创建一个球体
前面创建了圆柱体,接下来我们来创造一个球体。首先复制Cylinder函数,然后重命名为Sphere。我们可以通过将圆柱体的两级上的点挤压到一起,达到创造一个球体的目的。使用公式 $R = cos(\frac{πv}{2})$
public static Vector3 Sphere (float u, float v, float t) {
Vector3 p;
float r = Mathf.Cos(pi * 0.5f * v);
p.x = r * Mathf.Sin(pi * u);
p.y = v;
p.z = r * Mathf.Cos(pi * u);
return p;
}
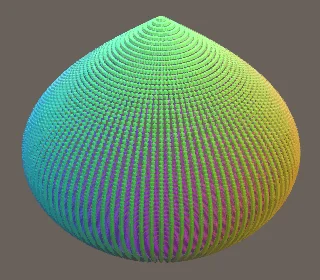
有点接近了,但还不是个正常的球。这是因为,一个圆,需要同时使用sine和cosine,而我们目前只使用了cosine,也就是上面 r 的值。所以,还需要在Y上使用sine。也就是 $sin(\frac{πv}{2})$
p.y = Mathf.Sin(pi * 0.5f * v);
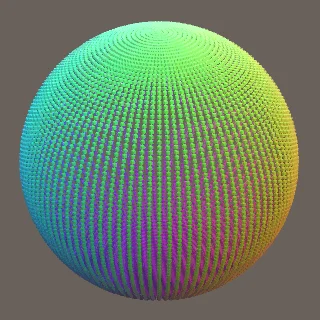
上面的球体其实是不均匀的,因为我们是通过堆叠不同半径的圆而构造出来的。
为了控制球体的半径,进而方便改变形状,我们将修改公式,使用 $f(u,v) = \begin{bmatrix} Ssin(πu)\\Rsin(\frac{πv}{2})\\Scos(πu)\end{bmatrix}$。而 $S = Rcos(\frac{πv}{2})$,R 是半径。
为了使用动画控制球体的半径,这次我们将对u和v分开使用sine函数。 $R = \frac{4}{5} + \frac{sin(π(6u + t))}{10} + \frac{sin(π(4v + t))}{10}$
float r = 0.8f + Mathf.Sin(pi * (6f * u + t)) * 0.1f;
r += Mathf.Sin(pi * (4f * v + t)) * 0.1f;
float s = r * Mathf.Cos(pi * 0.5f * v);
p.x = s * Mathf.Sin(pi * u);
p.y = r * Mathf.Sin(pi * 0.5f * v);
p.z = s * Mathf.Cos(pi * u);
3.4 创建一个环面
首先,复制 Sphere 函数,然后改名为 Torus
public static Vector3 Torus (float u, float v, float t) {
Vector3 p;
float s = Mathf.Cos(pi * 0.5f * v);
p.x = s * Mathf.Sin(pi * u);
p.y = Mathf.Sin(pi * 0.5f * v);
p.z = s * Mathf.Cos(pi * u);
return p;
}
首先,给s添加一个常数,例如 0.5
float s = Mathf.Cos(pi * 0.5f * v) + 0.5f;
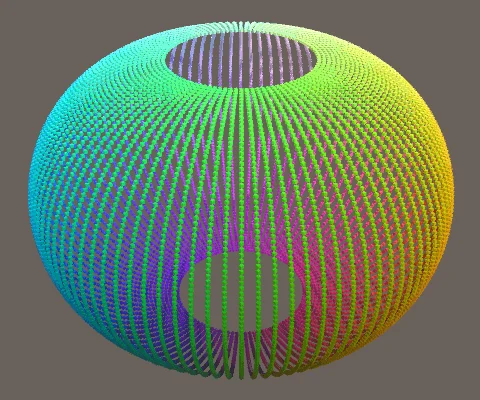
现在,我们得到了半个环面,接下来,我们需要使用v来描述整个圆。
float s = Mathf.Cos(pi * v) + 0.5f;
p.x = s * Mathf.Sin(pi * u);
p.y = Mathf.Sin(pi * v);
p.z = s * Mathf.Cos(pi * u);
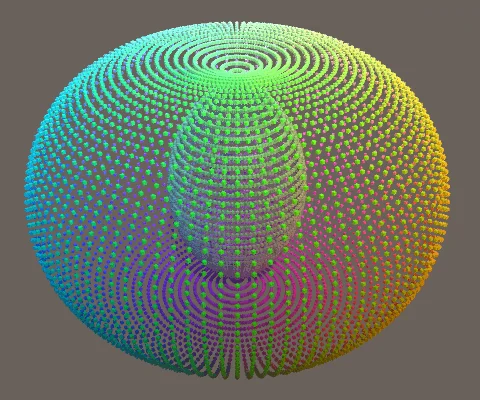
接下来,我们需要将公式变为,$f(u,v) = \begin{bmatrix}Ssin(πu)\\sin(πv)\\Scos(πu)\end{bmatrix}$,而 $S = cos(πv) + R_1$
float r1 = 1f;
float s = Mathf.Cos(pi * v) + r1;
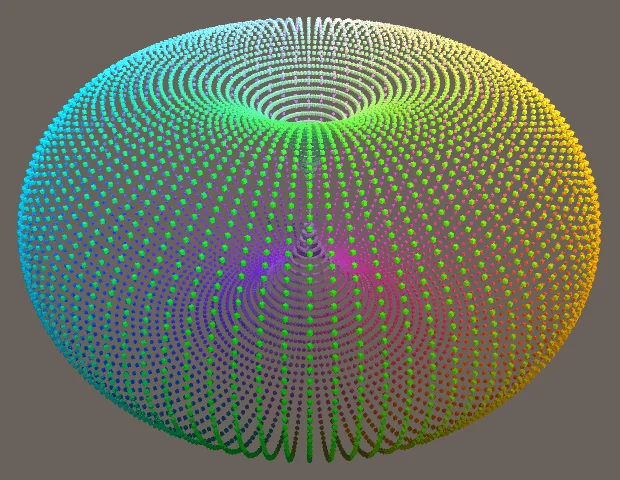
使$R_1$大于等于1,将在环面的中间打开一个洞,也就是说会形成一个圆环。我们再添加一个值,$R_2$用于控制圆环半径。$f(u,v) = \begin{bmatrix}Ssin(πu)\\R_2sin(πv)\\Scos(πu)\end{bmatrix}$,而$S=R_2cos(πv) + R_1$
我们将$R_1$设为1,$R_2$设为0.5
float r1 = 1f;
float r2 = 0.5f;
float s = r2 * Mathf.Cos(pi * v) + r1;
p.x = s * Mathf.Sin(pi * u);
p.y = r2 * Mathf.Sin(pi * v);
p.z = s * Mathf.Cos(pi * u);
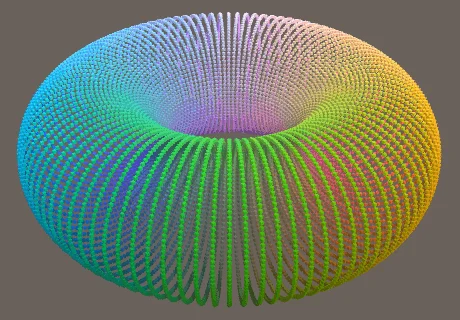
接下来就是添加动画,要注意一点是,需要确保环面在[-1,1]之间
float r1 = 0.65f + Mathf.Sin(pi * (6f * u + t)) * 0.1f;
float r2 = 0.2f + Mathf.Sin(pi * (4f * v + t)) * 0.05f;
到此,使用Unity实现漂亮的数学曲面结束。
原文翻译自 Mathematical Surfaces Sculpting with Numbers Github 代码下载 leaving-the-grid